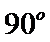- 空间中直线与直线之间的位置关系
- 共37题
19.(本小题满分12分)




(I)证明:
(II)求二面角
正确答案
知识点
α、β是两个平面,m、n是两条直线,有下列四个命题:
①如果m⊥n,m⊥α,n∥β,那么α⊥β.
②如果m⊥α,n∥α,那么m⊥n.
③如果α∥β,m
④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.
其中正确的命题有 .(填写所有正确命题的编号)
正确答案
②③④
知识点
如图,在三棱柱








22.求

23.求证:

24.求三棱锥
正确答案
见解析
解析
证明:∵底面三边长













考查方向
解题思路
第一问由线面垂直证明线线垂直,第二问由线线平行证明线面平行,第三问根据三棱锥体积的计算公式,先求出三棱锥底面面积,再找到高,进而求解。
易错点
直线与平面的关系的判断与证明,逻辑错误
正确答案
见解析
解析
证明:设







∴






考查方向
解题思路
第一问由线面垂直证明线线垂直,第二问由线线平行证明线面平行,第三问根据三棱锥体积的计算公式,先求出三棱锥底面面积,再找到高,进而求解。
易错点
直线与平面的关系的判断与证明,逻辑错误
正确答案
见解析
解析
解:取


∵



又∵



∴

∵
∴
考查方向
解题思路
第一问由线面垂直证明线线垂直,第二问由线线平行证明线面平行,第三问根据三棱锥体积的计算公式,先求出三棱锥底面面积,再找到高,进而求解。
易错点
直线与平面的关系的判断与证明,逻辑错误
如图,已知四棱锥P-ABCD,底面ABCD为蓌形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC 的中点.
21.求证:AE⊥PD;
22.若直线PB与平面PAD所成角的正弦值为
正确答案
见解析
解析
证明:由四边形



因为E为BC的中点,所以AE⊥BC.又BC∥AD,因此AE⊥AD.
因为PA

而PA

所以 AE⊥平面PAD,又PD
考查方向
解题思路
第1问通过线面垂直证明线线垂直,第2问先找到二面角的平面角,然后在根据相关线段长求二面角的余弦值。
易错点
计算错误;空间直角坐标系建立错误
正确答案
见解析
解析
由21知AE,AD,AP两两垂直,以








所以




由





解得



设平面AEF的一法向量为m=(x1,y1,z1),则







所以

因为二面角E-AF-C为锐角,所以所求二面角的余弦值为
考查方向
解题思路
第1问通过线面垂直证明线线垂直,第2问先找到二面角的平面角,然后在根据相关线段长求二面角的余弦值。
易错点
计算错误;空间直角坐标系建立错误
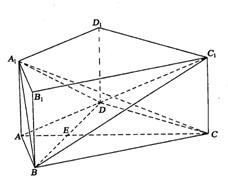
如图, 在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,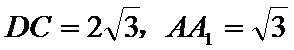
AD⊥DC,AC⊥BD, 垂足为E
20.求证:BD⊥A1C;
21.求二面角A 1-BD-C 1的大小;
正确答案
略
解析
在直四棱柱
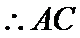

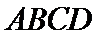
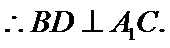
考查方向
解题思路
要证BD⊥A1C,可以寻找三垂线定理模型。
易错点
对垂直的论证不充分,不能充分应用图形的特点建系,在应用向量解决二面角问题时,思路不清晰。
正确答案
解析
连结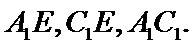
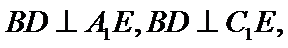

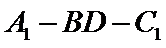
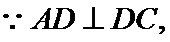
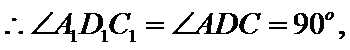
又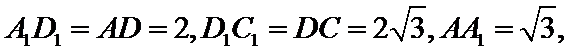
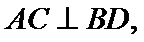
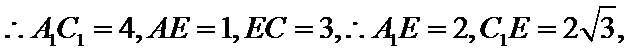
在
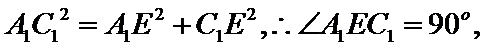
即二面角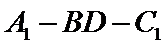

考查方向
解题思路
方法一:可以直接论证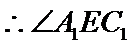

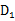
易错点
对垂直的论证不充分,不能充分应用图形的特点建系,在应用向量解决二面角问题时,思路不清晰。
扫码查看完整答案与解析