- 充要条件的判定
- 共176题
3. “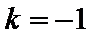
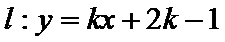
正确答案
解析
把直线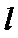
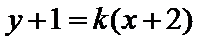
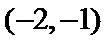
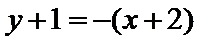
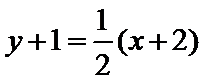
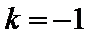
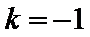
考查方向
解题思路
根据题意将直线化为点斜式方程,结合图象进行分析;
易错点
1、本题易在不理解充分条件与必要条件的含义而导致错误。
2、本题容易忽略直线在坐标轴上的截距为0而错选B。
知识点
16.下列说法中所有正确的序号是________
①、
②、若
③、
④、数列
正确答案
①③④
解析
对于①,

对于②,



对于③,由题意知




对于④,








考查方向
解题思路
逐个判断真假即可。
易错点
1. ②中很容易选错,③感觉无从下手;
2.对于④的单调性不能很好的利用对勾函数的单调性导致无法判断。
知识点
7.定义在






正确答案
解析
由






因为对任意的


















若





















考查方向
解题思路
本题属于中等题,可使用数形结合法,
(1)由

(2)由




(3)利用图形可得结论。
易错点
不会利用已知条件求函数的对称轴,不会判断函数的单调性,搞不清充分条件与必要条件。
知识点
2.设p: 




正确答案
解析




考查方向
解题思路
本题属于简单题,
(1)分别求解不等式,
(2)通过范围找出答案
易错点
计算过程对命题范围小的一方可以推出命题范围较大的一方,易理解为范围大推范围小
知识点
4.在数列



正确答案
解析
当数列














考查方向
解题思路
1.举特例(



2.再由等比中项,判定“对任意的


3.下结论。
易错点
本题易在判定是否为充分条件时出现错误,易忽视”数列为常数列0“的情形。
知识点
16. 设



正确答案
解析

由余弦函数的单调性可知
因为
所以“

考查方向
解题思路
本题考查平面向量的基础知识,直接运算即可。把条件判断转化为集合关系的判断更有利于解题。
易错点
本题必须注意充要条件的判定的方向性,A是B的XX条件和A的XX条件是B要区分清楚,忽视则会出现错误。
知识点
4.已知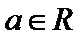
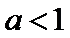
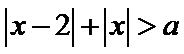
正确答案
解析
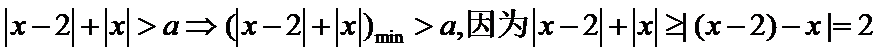
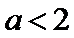
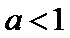
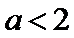
考查方向
解题思路
【解题思路】本题属于简单题,可使用直接法,
易错点
该题容易把恒成立问题的转换求错,对充分、必要条件的判定不熟导致选错
知识点
4.设函数f(x)=3x+bcosx,x∈R,则“b=0”是“函数f(x)为奇函数”的( )
正确答案
解析
若b=0,则f(x)=3x为奇函数,则充分性成立,
若函数f(x)为奇函数,则f(﹣x)=﹣3x+bcosx=﹣3x﹣bcosx,即b=﹣b,解得b=0,
即“b=0”是“函数f(x)为奇函数”充分条件和必要条件,
故选:C
考查方向
解题思路
等价转换“函数f(x)=3x+bcosx为奇函数”这句话为b=0再去判断。
易错点
本题易在“函数f(x)=3x+bcosx为奇函数”的化简上出错。
知识点
16.设



正确答案
解析
由已知得
∴
设
∵


即“

考查方向
本题主要考查了充分必要条件中的子集与推出关系以及向量的运算,考查学生分析问题的能力与计算能力,属于容易题,也是易错题.充分必要条件的问题在近几年的各省高考题中出现的频率非常高,可以与高中数学每一个章节每一个知识点相结合进行命题,是高考的热点问题.
解题思路
先利用向量的知识求出“

易错点
1.在向量的运算中,模运算可以转化为数量积的运算(
2.利用子集与推出关系来解决充分必要条件问题时,对子集与推出关系的不理解;
3.在充分必要条件问题中,容易混淆条件与结论.
知识点
15.设函数f (x)的定义域为I,若对

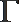
①f (x) =ln(l+x)(x≠0)为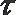
②f (x) =sinx (0<x<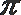
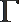
③f (x)为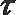

④f (x) =ax2-1既是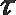
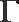
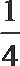
其中真命题有 .(把你认为真命题的序号都填上)
正确答案
①②④
解析
试题分析:本题属于函数图像的问题,题目的难度较大。注意严格按照题目的定义求解。
考查方向
本题主要考查了函数图像的问题。
解题思路
本题考查函数图像,解题步骤如下:依次画出①②③④中的函数图像,若满足f(x)<x,则称f(x)为T-函数;若有f[f(x)]<x,则称f(x)为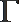
易错点
本题必须注意严格按照题目的定义求解,忽视则会出现错误。
知识点
扫码查看完整答案与解析














