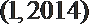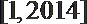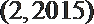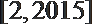两条直线垂直的判定
共92题

· 两条直线垂直的判定

两条直线垂直的判定
共92题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

27．已知函数.

（1）要使在区间上单调递增，试求的取值范围；

（2）当时，试求的解析式，使的极大值为，极小值为1。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两条直线垂直的判定

题型：单选题

单选题 · 5 分

4．已知直线⊥平面，直线m，给出下列命题：

①∥

②∥m;

③∥m

④∥

其中正确的命题是（）

A①②③

B②③④

C②④

D①③

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两条直线垂直的判定

题型：填空题

填空题 · 4 分

22. 在中，若，则值等于（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两条直线垂直的判定

题型：简答题

简答题 · 12 分

20.已知二次函数y＝f(x)的图象经过坐标原点，其导函数为＝6x－2，数列{an}的前n项和为Sn，点(n，Sn)(n∈N*)均在函数y＝f(x)的图象上。

（1）求数列{an}的通项公式；

（2）设bn＝，Tn是数列{bn}的前n项和，求使得Tn＜对所有n(n∈N*)都成立的最小正整数m。

正确答案

解　（1）设函数f(x)＝ax2＋bx(a≠0)，

则f′(x)＝2ax＋b，由f′(x)＝6x－2，

得a＝3，b＝－2，所以f(x)＝3x2－2x.

又因为点(n，Sn)(n∈N*)均在函数y＝f(x)的图象上，

所以Sn＝3n2－2n.

当n≥2时，an＝Sn－Sn－1＝(3n2－2n)－[3(n－1)2－2(n－1)]

＝6n－5.

当n＝1时，a1＝S1＝3×12－2×1＝1，所以，an＝6n－5(n∈N*)．

解析

解析已在路上飞奔，马上就到！

知识点

两条直线垂直的判定

题型：填空题

填空题 · 4 分

4．已知函数f（x）的图象与函数的图象关于直线y=x对称，则f（9）= （）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两条直线垂直的判定

题型：单选题

单选题 · 4 分

15．函数y=（）

A在（-，+）上单调递增。

B在上是减函数，在上是增函数。

C在上是增函数，在上是减函数。

D在上是减函数，在上是增函数。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两条直线垂直的判定

题型：简答题

简答题 · 14 分

19.已知F1，F2分别是椭圆＋＝1的左、右焦点，曲线C是以坐标原点为顶点，以F2为焦点的抛物线，自点F1引直线交曲线C于P、Q两个不同的交点，点P关于x轴的对称点记为M.设＝λ

（Ⅰ）求曲线C的方程；

（Ⅱ）证明：＝－λ；

（Ⅲ）若λ∈[2,3]，求|PQ|的取值范围.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两条直线垂直的判定

题型：简答题

简答题 · 12 分

17．已知函数和的图象关于y轴对称，且

（I）求函数的解析式；

（II）解不等式；

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两条直线垂直的判定

题型：单选题

单选题 · 5 分

12.已知函数，若互不相等，且，则的取值范围是（）

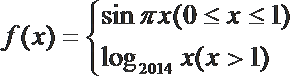
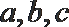
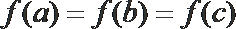
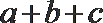
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两条直线垂直的判定

题型：填空题

填空题 · 5 分

选做题：第14、15题是选做题，只能选做一题，两题全答的，只计算第14题的得分．

14．已知⊙O1和⊙O2交于点C和D，⊙O1上的点P处的切线交⊙O2于A、B点，交直线CD于点E，M是⊙O2上的一点，若PE=2，EA=1，AMB=30o，那么⊙O2的半径为_________．

15．在极坐标系中，圆的圆心到直线的距离是_______．

正确答案

14. 3

15.

解析

解析已在路上飞奔，马上就到！

知识点

两条直线垂直的判定

继续学习学习下一知识点

下一知识点 : 两条直线垂直与倾斜角、斜率的关系

百度题库 > 高考 > 理科数学 > 两条直线垂直的判定

扫码查看完整答案与解析