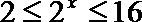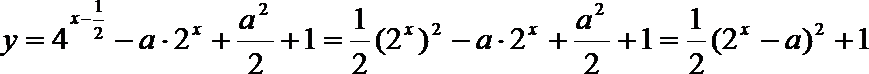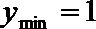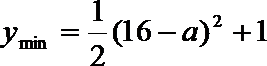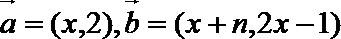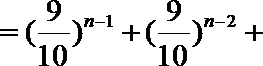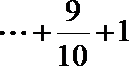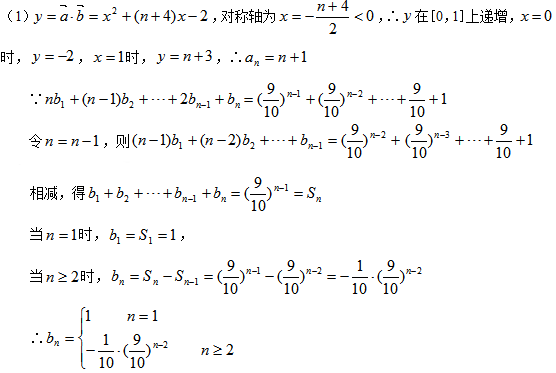- 二次函数在闭区间上的最值
- 共44题
17.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设函数




正确答案
[-3,6]
解析
解析已在路上飞奔,马上就到!
知识点
20.设二次函数



(1)求函数
(2)若对于任意的


正确答案
(1)设
∵ 

∴
∴
(2)
∴
即
解析
解析已在路上飞奔,马上就到!
知识点
7.已知直线x=a(0<a<

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知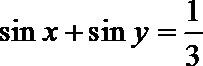
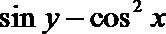
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知函数





(1)求

(2)若不等式


正确答案
解:(1)
因为



故

(2)由(1)可得
所以

可化为

即
令


记

因为

故当

所以

解析
解析已在路上飞奔,马上就到!
知识点
20.已知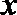
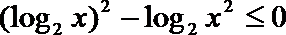
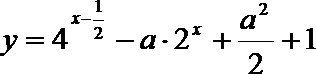
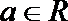
正确答案
解不等式 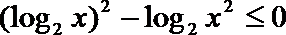
得 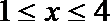
所以
当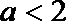
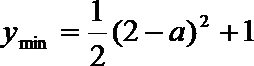
当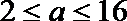
当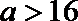
解析
解析已在路上飞奔,马上就到!
知识点
6.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知椭圆C的焦点在x轴上,中心在原点,离心率

(I)求椭圆C的方程;
(II)设椭圆C的左.右顶点分别为A1,A2,点M是椭圆上异于Al,A2的任意一点,设直线MA1,MA2的斜率分别为

(III)设椭圆方程


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设向量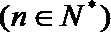
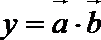
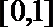
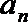
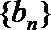
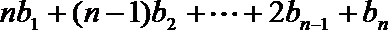
(1)求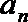
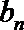
(2)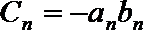
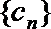
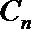
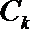
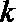
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析