- 对数函数的定义
- 共62题
16.若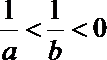
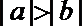
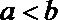
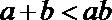
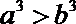
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.函数

(Ⅰ)当


(Ⅱ)如果函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若对任意的实数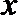
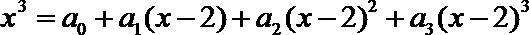
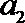
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数f(x)=ax3+bsin x+4(a,b∈R),f(lg(log210))=5,则f(lg(lg 2))=( )
正确答案
解析
因为log

所以lg(log



知识点
2.设集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列{an}中,a1=2,a2=3,其前n项和Sn满足Sn+1+Sn-1=2Sn+1(n≥2,n∈N*).
(1) 求数列{an}的通项公式;
(2) 设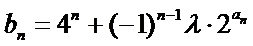
正确答案
(1) 由已知,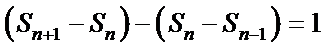
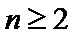
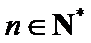
即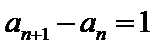
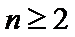
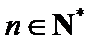
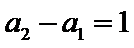
∴数列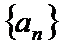
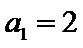
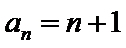
(2) ∵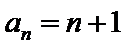
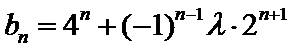
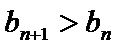
即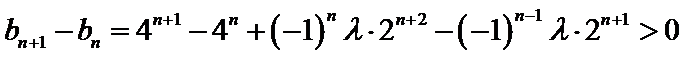
∴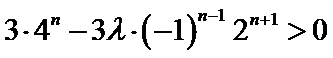
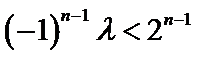
1°当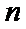
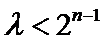
∵当且仅当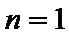
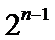
2°当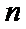
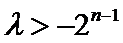
∵当且仅当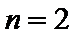
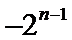
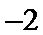
故-2<λ<1,又λ为非零整数,则λ=-1.
综上所述,存在λ=-1,使得对任意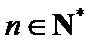
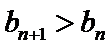
解析
解析已在路上飞奔,马上就到!
知识点
14.以双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设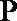
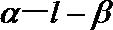
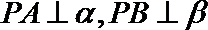
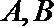
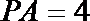
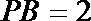
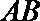
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 对于函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析