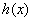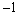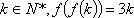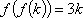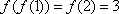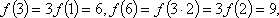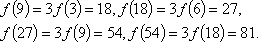- 函数的概念与基本初等函数
- 共8430题
对于函数










(1)若


(2)若





(3)若


①




正确答案
见解析
解析
(1)由题


可得

故


(2)当



解得


故


又


当



故



当



所以当



当




当




(3)由


即


即

所以

故

若


由

又

知识点
已知函数



正确答案
解析
略
知识点
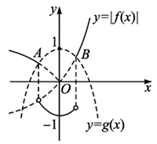
已知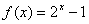
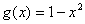
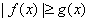
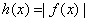
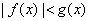
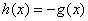
正确答案
解析
画出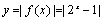
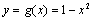
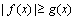
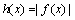
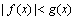
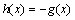
综上可知, 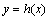
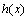
知识点
甲乙两人从4门课程中各选修2门,则甲乙两人所选的课程中恰有1门相同的选法有
正确答案
解析
略
知识点
如图3,AB的延长线上任取一点C,过C作圆的切线CD,切点为D,

正确答案
45°
解析
连接











知识点
函数

正确答案
2
解析
略
知识点
已知幂函数
(1)求
(2)求满足
正确答案
见解析。
解析
(1)∵幂函数
∴


其图象关于y轴对称,∴符合;当m=2时,
(2)∵m=1,满足
∴


∴
从而

知识点
已知函数
(1)求此函数的单调区间及最值;
(2)求证:对于任意正整数n,均有

(3)当a=1时,是否存在过点(1,-1)的直线与函数
正确答案
见解析。
解析
(1)解:由题意
当


此时函数在


当


此时函数在


(2)取

故
取

(3)假设存在这样的切线,设其中一个切点
∴切线方程:



设






故
又
注意到


方程①有且仅有一解,故符合条件的切线有且仅有一条,…………14分
知识点
若对于定义在







正确答案
解析
A正确,令











B错误,用反证法,假设






C错误.因为
D错误,设





知识点
函数


正确答案
解析
略
知识点
已知函数

(1)求曲线

(2)若


(3)若对任意的




正确答案
(1)
(2)
(3)
解析
(1)
定义域

法一:令

又

经验证
法二:令








(2)对任意的

等价于对任意的

当














2)若
当
当







3)当





综上所述
知识点
已知函数



正确答案
解析
由已知得
知识点
已知函数

正确答案
解析
∵


知识点
对于定义域为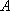
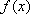
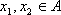
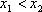
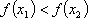
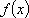
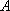
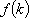
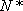
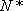
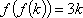
(1)证明: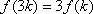
(2)求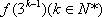
(3)是否存在p个连续的自然数,使得它们的函数值依次也是连续的自然数;若存在,找出所有的p值,若不存在,请说明理由.
正确答案
见解析
解析
(1)证明:对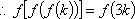
由已知
由①、②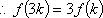
(2)若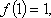
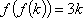
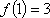
设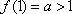
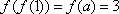
由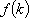
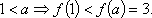

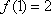
由③有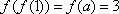
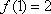
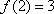
依此类推归纳猜出: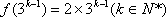
下面用数学归纳法证明:
(1)当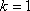
(2)假设当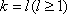
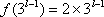
那么当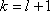
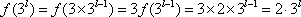
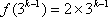
(3)存在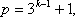
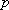
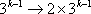
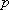
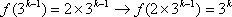
知识点
设函数
(1)求函数
(2)若函数



正确答案
见解析。
解析
(1)函数

令

①当





②当







③当








故当







(2)∵



故此时



设

则
由于



故
∴
知识点
扫码查看完整答案与解析