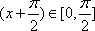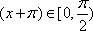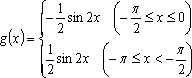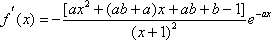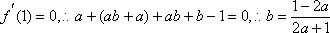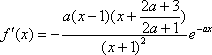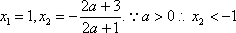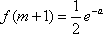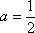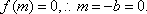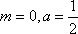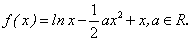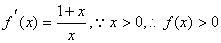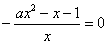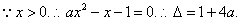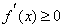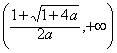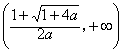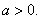- 函数的概念与基本初等函数
- 共8430题
已知实数

(1)当

(2)当

(3)求实数



正确答案
(1)2(2)递增(3)
解析
解析:易知


(1)



(2)







设

所以

(3)

从而原问题等价于求实数

恒有
①当





从而
②当




由


③当




由


④当


由


综上,
知识点
函数f(x)=|x﹣2|﹣lnx在定义域内零点的个数为( )
正确答案
解析
由题意,函数f(x)的定义域为(0,+∞);
由函数零点的定义,f(x)在(0,+∞)内的零点即是方程|x﹣2|﹣lnx=0的根.
令y1=|x﹣2|,y2=lnx(x>0),在一个坐标系中画出两个函数的图象:
由图得,两个函数图象有两个交点,
故方程有两个根,即对应函数有两个零点.
故选C.
知识点
方程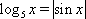
正确答案
解析
略
知识点
定义域为







(1)判断函数

(2)如果函数


(3)对于区间






① 证明: 当


② 请再选一个与①不同的且大于1的整数
证明:
正确答案
见解析
解析
解析:(1)设






(2)对于




………………7分
若

若



综上所述得
(3)①当

假设当

那么,由
得

即
②比如证明




有





从而得
知识点
在点

正确答案
解析
函数






知识点
“活水围网”养鱼技术具有养殖密度高、经济效益好的特点,研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度











(1)当

(2)当养殖密度


正确答案
(1)
解析
解析:(1)由题意:当

当



由已知得

故函数

(2)依题意并由(1)可得
当


当


所以,当


当养殖密度为10尾/立方米时,鱼的年生长量可以达到最大,最大值约为
…………………………14分
知识点
设函数
(1)当


(2)设


(3)设



正确答案
见解析
解析
解析:(1)


所以
(2)证明:因为 









(3)当n=2时,f2(x)=x2+bx+c.
对任意x1,x2∈[-1,1]都有|f2(x1)-f2(x2)|≤4等价于f2(x)在[-1,1]上的
据此分类讨论如下:
①当
②当-1≤


③当0≤


综上可知,-2≤b≤2.
注:②,③也可合并证明如下:
用max{a,b}表示a,b中的较大者。
当


=
=1+c+|b|-(
=(1+
知识点
如图,设







(1)求点

(2)若

正确答案
(1)
解析
解析:(1)当

所以
所以,点B的坐标是(0,1) ……………………………………………………2分
又


(2)由


又





所以,

知识点
已知函数
(1)当
(2)设

(3)设

正确答案
见解析。
解析
(1)当
令

当
当
∴当

(2)解法一:
函数

将方程

当
解得

即当

当

则
令


当


∴当

即对
∵当
当
∴函数
∴当

∴当


当


当


当


综上得:当

当

当


解法二:
当



当



∴若



若

当


∴当



当



当

令
∴函数

∴当

综上得:当

当

当


(3)由(1)知对


即
知识点
已知函数

正确答案
解析
略
知识点
已知函数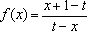

(1)当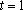
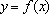
(2)设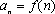
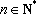
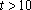
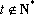
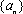
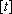

(3)利用函数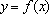
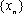
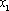
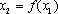
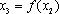
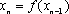
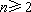
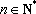
在上述构造过程中,若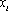
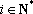
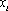
若取定义域中的任一值作为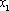
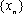

正确答案
见解析
解析
(1)当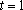
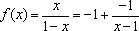
图像如图(2分)
基本性质:(每个2分)
奇偶性:既非奇函数又非偶函数;
单调性:在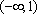
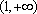
零点: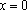
最值:无最大、小值,(6分)
(2)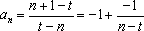
当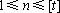
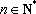
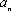
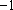
当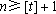
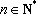
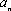
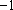
因此,数列中的最大项为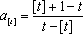
最小项为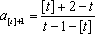
(3)由题意,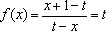
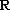
亦即当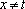
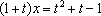
由于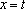
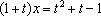
因此对任意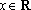
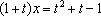
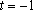
知识点
设函数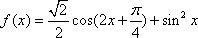
(1)求函数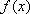
(2)设函数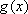
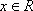
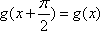
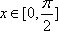
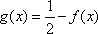
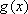

正确答案
(1)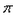
解析
解析: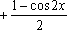
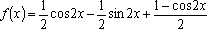
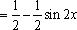
(1)函数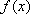
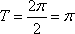

(2)当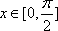
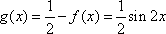
当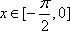
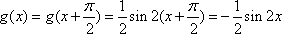
当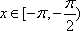
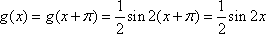
得函数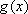
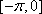
知识点
设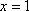
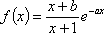
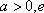
(1)求
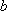

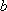
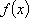
(2)若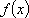
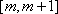
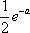
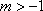
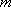

正确答案
见解析。
解析
(1)
由已知有:
从而
令
当
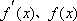
从上表可知: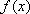
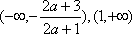
在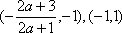
(2)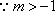
①当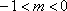
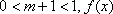
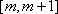
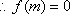
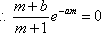
解得
又
故此时的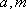
②当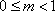
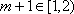
将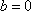
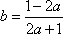
又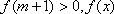
③当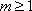
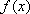
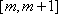
又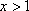
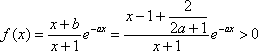
∴此时的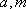
综上所述
知识点
设函数



(1)证明:
(2)当


(3)证明:

正确答案
见解析
解析
(1)证明:设
当





即函数



因为


即

(2)解:当

用数学归纳法证明如下:
①当

②假设当


令

因为对任意的正实数

由归纳假设知,
即


因为

从而对任意

即对任意

这就是说,当


由①、②知,当

(3)先证对任意正整数

由(2)知,当


令


再证对任意正整数

要证明上式,只需证明对任意正整数

即要证明对任意正整数

①当

②假设当

即
则
因为
所以
这说明当
由①、②知,对任意正整数
综上可知,对任意正整数

知识点
已知函数
(1)求函数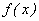
(2)是否存在实数a,使得函数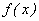
正确答案
见解析
解析
(1)解:函数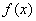

①当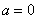
∴函数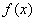
②当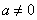
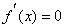
(i)当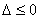
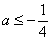
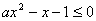
∴函数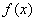
(ii)当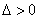
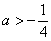
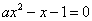
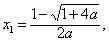
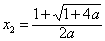
若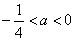
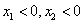
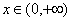
∴函数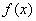
若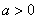
此时,当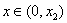
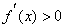
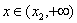
∴函数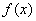
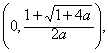
综上所述,当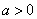
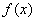
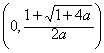
为
当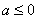
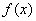
(2)解:由(1)得当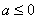
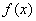
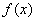
当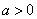
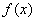
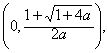
则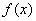
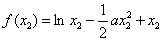
而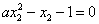
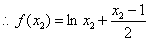
设函数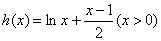
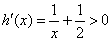
则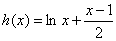
又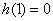
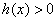
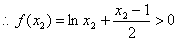
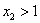
即在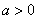
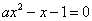
设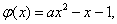
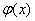
轴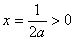
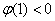
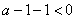
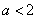
故实数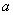
说明:若采用下面的方法求出实数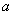
(i),由于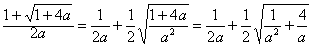
而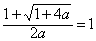
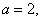
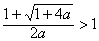
从而实数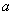
(ii)直接解不等式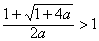
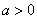
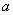
(0,2)。
知识点
扫码查看完整答案与解析