- 平行向量与共线向量
- 共100题
如图,游客从某旅游景区的景点A处下山至C处有两种路径,一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.
现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min,在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130 m/min,山路AC长为1 260 m,经测量,cos A=

(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
正确答案
(1) 1 040(m) ;(2) 
解析
(1)在△ABC中,因为cos A=



从而sin B=sin[π-(A+C)]=sin(A+C)=sin Acos C+cos Asin C=
由正弦定理

所以索道AB的长为1 040 m.
(2)假设乙出发t min后,甲、乙两游客距离为d,此时,甲行走了(100+50t) m,乙距离A处130t m,
所以由余弦定理得d2=(100+50t)2+(130t)2-2×130t×(100+50t)×
因0≤t≤

(3)由正弦定理

乙从B出发时,甲已走了50×(2+8+1)=550(m),还需走710 m才能到达C.
设乙步行的速度为v m/min,由题意得


知识点
已知



正确答案
解析
略。
知识点
如图,在平面直角坐标系xOy中,M,N分别是椭圆

(1)若直线PA平分线段MN,求k的值;
(2)当k=2时,求点P到直线AB的距离d;
(3)对任意的k>0,求证:PA⊥PB.
正确答案
见解析
解析
(1)由题设知,a=2,b=




(2)直线PA的方程为y=2x,代入椭圆方程得




于是C


因此,
(3)解法一:将直线PA的方程y=kx代入



故直线AB的斜率为

解得

于是直线PB的斜率
因此k1k=-1,所以PA⊥PB.
解法二:设P(x1,y1),B(x2,y2),则x1>0,x2>0,x1≠x2,A(-x1,-y1),C(x1,0).设直线PB,AB的斜率分别为k1,k2.因为C在直线AB上,所以
因此k1k=-1,所以PA⊥PB.
知识点
已知函数



正确答案
解析
取x=1 y=0得
法一:通过计算
法二:取x=n y=1,有f(n)=f(n+1)+f(n-1),同理f(n+1)=f(n+2)+f(n)
联立得f(n+2)= —f(n-1) 所以T=6 故
知识点
已知动点P,Q都在曲线C:
(1)求M的轨迹的参数方程;
(2)将M到坐标原点的距离d表示为α的函数,并判断M的轨迹是否过坐标原点。
正确答案
(1) 
解析
(1)依题意有P(2cos α,2sin α),Q(2cos 2α,2sin 2α),
因此M(cos α+cos 2α,sin α+sin 2α)。
M的轨迹的参数方程为
(2)M点到坐标原点的距离

当α=π时,d=0,故M的轨迹过坐标原点。
知识点
若集合

正确答案
解析

知识点
已知f(x)=m(x-2m)(x+m+3),g(x)=
①
②
则m的取值范围是
正确答案
解析
根据


































知识点
设集合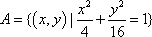
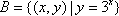
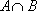
正确答案
解析
画出椭圆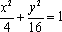
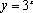

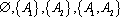
知识点
设
正确答案
解析
略。
知识点
设变量x,y满足约束条件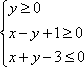
正确答案
解析
略
知识点
扫码查看完整答案与解析