- 函数与方程
- 共222题
17.函数f(x)=x3-3ax2+3bx的图象与直线12x+y-1=0相切于点(1,-11)
(1)求a、b的值;
(2)方程f(x)=c有三个不同的实数解,求c的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
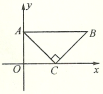
14.如图放置的等腰直角三角形ABC薄片(∠ACB=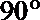
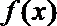
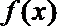
正确答案
2+4
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(Ⅰ)若


(Ⅱ)若


正确答案
解:(Ⅰ)
①当


得


②当


得

综合①,②得b的取值范围是
(Ⅱ)令
当


∵


∴

当


∴

又因为函数

∴
∵


则

当a≥3时,
∴g(x)=0在
当

∴g(x)=0在
解析
解析已在路上飞奔,马上就到!
知识点
14.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数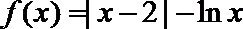
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数f(x)= 
正确答案
解析
当x≤0时,
令
当x>0时,令
4-x+ln x=0⇒ln x=x-4,
通过图象可知有两个交点,此时也有两个根.
所以已知函数有4个零点.
知识点
12.已知函数f(x)是定义在R上的奇函数,并满足f(x-4)=-f(x)且在[0,2]上是增函数,给出下列结论:
(1)若0<x1<x2<4,且x1+x2=4,则f(x1)+f(x2)>0;
(2)若0<x1<x2<4,且x1+x2=5,则f(x1)>f(x2);
(3)若方程f(x)=m在[-8,8]内恰有四个不同的根x1,x2,x3,x4,则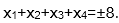
正确答案
解析
∵f(x-4)=-f(x),
∴f(x-8)=-f(x-4)=f(x),
∴f(x)的周期为8.
∵函数f(x)是定义在R上的奇函数,
∴f(x)关于原点对称.
∵f(x-4)=-f(x),∴f(x-4)=f(-x),
∴f(x)关于x=-2对称.
由f(x)关于原点对称,
∴f(x)也关于x=2对称.
由f(x)在[0,2]上是增函数,且f(0)=f(4)=0,则可以画出草图为
(1)若0<x1<x2<4,且x1+x2=4,则可得到x1,x2关于x=2对称,
由图可知f(x1)>0,f(x2)>0,
所以f(x1)+f(x2)>0,故(1)正确.
(2)若0<x1<x2<4,且x1+x2=5,则可得x2到x=2的距离比x1到x=2的距离要远,
由图象可得f(x1)>f(x2),故(2)正确.
(3)如图所示,若m>0,则两个根关于x=-6对称,两个根关于x=2对称,
所以有x1+x2+x3+x4=-8.若m<0,
则两个根关于x=-2对称,
两个根关于x=6对称,所以有x1+x2+x3+x4=8,
故(3)也正确.
本题答案为D.
知识点
6.设方程x4+ax-4=0的各实根为x1,x2,…,xk(k≤4).若点(xi,
正确答案
解析
因为x4+ax-4=0,所以x≠0,所以x3+a=
由y=x,y=
考虑极限位置, 当y=x3+a过点(2,2)时,a=-6;
当y=x3+a过点(-2,-2)时,a=6,
所以若点(xi,
知识点
12.已知函数f(x)是定义在R上的奇函数,并满足f(x-4)=-f(x)且在[0,2]上是增函数,给出下列结论:
(1)若0<x1<x2<4,且x1+x2=4,则f(x1)+f(x2)>0;
(2)若0<x1<x2<4,且x1+x2=5,则f(x1)>f(x2);
(3)若方程f(x)=m在[-8,8]内恰有四个不同的根x1,x2,x3,x4,则
正确答案
解析
∵f(x-4)=-f(x),
∴f(x-8)=-f(x-4)=f(x),
∴f(x)的周期为8.
∵函数f(x)是定义在R上的奇函数,
∴f(x)关于原点对称.
∵f(x-4)=-f(x),∴f(x-4)=f(-x),
∴f(x)关于x=-2对称.
由f(x)关于原点对称,
∴f(x)也关于x=2对称.
由f(x)在[0,2]上是增函数,且f(0)=f(4)=0,则可以画出草图为
(1)若0<x1<x2<4,且x1+x2=4,则可得到x1,x2关于x=2对称,
由图可知f(x1)>0,f(x2)>0,
所以f(x1)+f(x2)>0,故(1)正确.
(2)若0<x1<x2<4,且x1+x2=5,则可得x2到x=2的距离比x1到x=2的距离要远,
由图象可得f(x1)>f(x2),故(2)正确.
(3)如图所示,若m>0,则两个根关于x=-6对称,两个根关于x=2对称,
所以有x1+x2+x3+x4=-8.若m<0,
则两个根关于x=-2对称,
两个根关于x=6对称,所以有x1+x2+x3+x4=8,
故(3)也正确.
本题答案为D.
知识点
扫码查看完整答案与解析