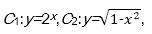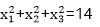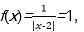- 函数与方程
- 共222题
1.方程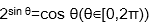
正确答案
解析
因为2sin θ>0,
所以cos θ>0,
令sin θ=x,-1≤x≤1,则问题转化为方程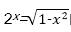
记
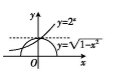
则问题又转化为两条曲线在x∈[-1,1]内交点个数的问题.
在同一坐标系中画出它们的图象,
如图所示
故选B.
知识点
7.方程(
正确答案
2
解析
如图,方程

.根据图象可得交点个数为2,
即解的个数为2.
知识点
1.已知函数f(x)=sin(2ωx+



正确答案
解析
因为f(x)相邻两条对称轴之间的距离为


又T=


将f(x)的图象向右平移
f(x)=sin[4(x-



令2x-



若g(x)+k=0在x∈[0,
即y=sin t与y=-k在[-

如图所示,由正弦函数的图象可知-



知识点
12.已知f(x)为偶函数,当x≥0时,f(x)=2a|x-1|-a(a>0),若函数y=f[f(x)]恰有10个零点,则a的取值范围为( ).
正确答案
解析
作出函数f(x)的图象,如图所示,因为当f(x)=0时,x=-









知识点
14.已知函数f(x)=|x2+3x|,x∈R.若方程f(x)-a|x-1|=0恰有4个互异的实数根,则实数a的取值范围为______.
正确答案
(0,1)
解析
设y1=f(x)=|x2+3x|,y2=a|x-1|,在同一直角坐标系中作出y1=|x2+3x|,y2=a|x-1|的图象,如图所示.
由图可知f(x)-a|x-1|=0恰有4个互异的实数根等价于y1=|x2+3x|与y2=a|x-1|的图象有4个不同的交点,且4个交点的横坐标都小于1,
所以
消去y,得x2+(3-a)x+a=0在x∈(-3,0)内有两个不同实根,
所以Δ=(3-a)2-4a>0,即a2-10a+9>0,
解得a<1或a>9(舍去).
又由图象得a>0,所以0<a<1.
知识点
9.已知函数y=f(x)的周期为2,当x∈[-1,1]时,f(x)=x2,那么函数y=f(x)的图象与函数y=|lg x|的图象的交点共有 个.
正确答案
10
解析
在同一坐标系中作出函数
由图象可知,两个函数的图象的交点共有10个.
知识点
7.设函数
正确答案
3
解析
由f(-4)=f(0),
得16-4b+c=c,且由对称性可知,
f(x)在x=-2处取得最小值,
即f(-2)=-2,得4-2b+c=-2.
联立方程解得b=4,c=2,
所以
在同一直角坐标系中作出函数y=f(x)与函数y=x的图象,知它们有3个交点,
即f(x)=x有3个根.
知识点
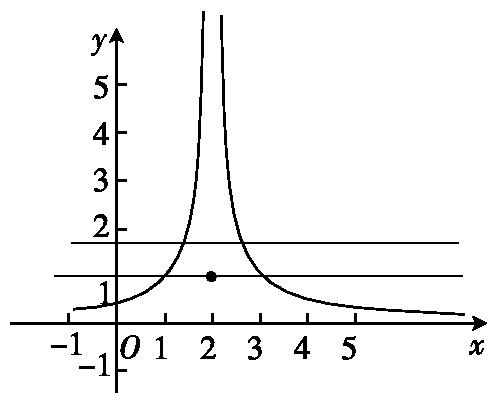
6.设定义域为R的函数f(x)= 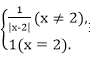
正确答案
解析
作出f(x)的图象(图略),
图象关于x=2对称,且当x=2时,
f(x)=1,故f(x)=1有三个不同实数根x,
除此之外,f(x)只有两个根或无根.
又f2(x)+af(x)+b=0有三个不同的实数
解x1<x2<x3,x2=2,
而x1+x3=2x2=4.又当x≠2时,
解得x1=1,x3=3,
故A,B,C正确.
知识点
8.已知函数
正确答案
解析
作出函数f(x)的图象如图,由图象可知,当
f(x1)=f(x2),
即
所以
令
由二次函数图象可知函数递增,
所以
即为x1f(x2)的取值范围.
知识点
5.定义在R上的函数f(x)=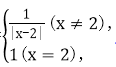
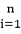
正确答案
解析
方程f2(x)-mf(x)+m-1=0的解是f(x)=1或f(x)=m-1>1.在坐标系中画出函数f(x)的图象,以及直线y=1,y=m-1(如图所示).由图象可知函数f(x)的图象与直线y=1,y=m-1有五个不同的公共点,即方程f2(x)-mf(x)+m-1=0有五个不同的实根.设x1<x2<x3<x4<x5,则x1+x5=x2+x4=4,x3=2,所以f(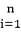


知识点
扫码查看完整答案与解析