- 函数与方程
- 共222题
已知函数f(x)=x3+ax2+b(a,b∈R).
25.试讨论f(x)的单调性;
26.若b=c﹣a(实数c是与a无关的常数),当函数f(x)有三个不同的零点时,a的取值范围恰好是(﹣∞,﹣3)∪(1,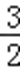
正确答案
函数f(x)在(﹣∞,0),(﹣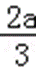
解析
(1)∵f(x)=x3+ax2+b,
∴f′(x)=3x2+2ax,
令f′(x)=0,可得x=0或﹣
a=0时,f′(x)>0,∴f(x)在(﹣∞,+∞)上单调递增;
a>0时,x∈(﹣∞,﹣

∴函数f(x)在(﹣∞,﹣
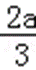
a<0时,x∈(﹣∞,0)∪(﹣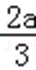
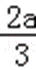
∴函数f(x)在(﹣∞,0),(﹣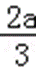
考查方向
解题思路
(1)求导数,分类讨论,利用导数的正负,即可得出f(x)的单调性;
易错点
本题考查导数知识的综合运用,考查函数的单调性,分类讨论中易错
正确答案
c=1
解析
(2)由(1)知,函数f(x)的两个极值为f(0)=b,f(﹣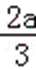
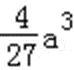
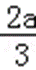
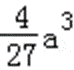
∵b=c﹣a,
∴a>0时,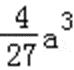
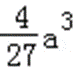
设g(a)=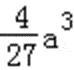
∵函数f(x)有三个不同的零点时,a的取值范围恰好是(﹣∞,﹣3)∪(1,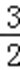
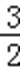
∴在(﹣∞,﹣3)上,g(a)<0且在(1,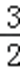
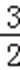
∴g(﹣3)=c﹣1≤0,且g(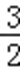
∴c=1,
此时f(x)=x3+ax2+1﹣a=(x+1)[x2+(a﹣1)x+1﹣a],
∵函数有三个零点,
∴x2+(a﹣1)x+1﹣a=0有两个异于﹣1的不等实根,
∴△=(a﹣1)2﹣4(1﹣a)>0,且(﹣1)2﹣(a﹣1)+1﹣a≠0,
解得a∈(﹣∞,﹣3)∪(1,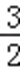
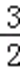
综上c=1.
考查方向
解题思路
(2)由(1)知,函数f(x)的两个极值为f(0)=b,f(﹣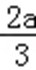
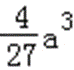
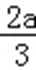
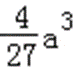
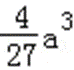
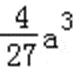
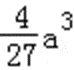
易错点
本题考查导数知识的综合运用,考查函数的单调性,考查函数的零点,在用范围的过程中易错.
已知函数f(x)=x3+ax2+b(a,b∈R).
25.试讨论f(x)的单调性;
26.若b=c﹣a(实数c是与a无关的常数),当函数f(x)有三个不同的零点时,a的取值范围恰好是(﹣∞,﹣3)∪(1,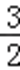
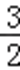
正确答案
函数f(x)在(﹣∞,0),(﹣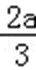
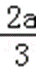
解析
(1)∵f(x)=x3+ax2+b,
∴f′(x)=3x2+2ax,
令f′(x)=0,可得x=0或﹣
a=0时,f′(x)>0,∴f(x)在(﹣∞,+∞)上单调递增;
a>0时,x∈(﹣∞,﹣

∴函数f(x)在(﹣∞,﹣
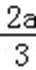
a<0时,x∈(﹣∞,0)∪(﹣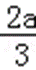
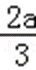
∴函数f(x)在(﹣∞,0),(﹣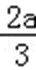
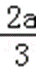
考查方向
解题思路
(1)求导数,分类讨论,利用导数的正负,即可得出f(x)的单调性;
易错点
本题考查导数知识的综合运用,考查函数的单调性,分类讨论中易错
正确答案
c=1
解析
(2)由(1)知,函数f(x)的两个极值为f(0)=b,f(﹣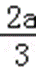
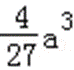
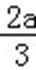
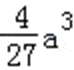
∵b=c﹣a,
∴a>0时,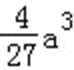
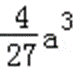
设g(a)=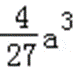
∵函数f(x)有三个不同的零点时,a的取值范围恰好是(﹣∞,﹣3)∪(1,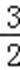
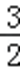
∴在(﹣∞,﹣3)上,g(a)<0且在(1,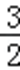
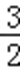
∴g(﹣3)=c﹣1≤0,且g(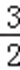
∴c=1,
此时f(x)=x3+ax2+1﹣a=(x+1)[x2+(a﹣1)x+1﹣a],
∵函数有三个零点,
∴x2+(a﹣1)x+1﹣a=0有两个异于﹣1的不等实根,
∴△=(a﹣1)2﹣4(1﹣a)>0,且(﹣1)2﹣(a﹣1)+1﹣a≠0,
解得a∈(﹣∞,﹣3)∪(1,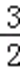
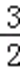
综上c=1.
考查方向
解题思路
(2)由(1)知,函数f(x)的两个极值为f(0)=b,f(﹣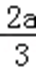
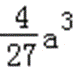
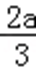
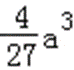
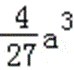
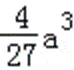
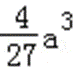
易错点
本题考查导数知识的综合运用,考查函数的单调性,考查函数的零点,在用范围的过程中易错.
4.设

正确答案
解析
因为
故f(x)为奇函数,
又
故选B.
考查方向
解题思路
利用函数奇偶性的定义和导数判断函数的单调性.
易错点
函数具有奇偶性的必要条件是其定义域关于原点对称。如果不具备这个条件,一定是非奇非偶函数。
知识点
()是会计职业组织对整个会计职业的会计行为进行自我约束、自我控制的过程。
A.会计人员自律
B.会计行业自律
C.会计队伍自律
D.会计主管自律
正确答案
B
解析
暂无解析
12.设函数





正确答案
解析
根据分段函数的解析式,作出图象,
当直线




考查方向
分段函数的性质
函数与方程的零点问题
解题思路
根据图象和方程的零点,然后求出M的取值范围
易错点
对函数的图象性质掌握不好,作图错误
知识点
除了宏观因素和微观因素外,其他影响个人理财活动的因素有( )。
A.客户对理财业务的认知度
B.金融机构监管体制
C.中介机构发展水平
D.其他理财机构理财业务的发展
E.商业银行个人理财业务定位
正确答案
A,B,C,D,E
解析
[解析] 除了宏观因素和微观因素外,个人理财活动主体的意识和行为以及其他一些因素都会直接和间接对商业银行个人理财业务产生影响。题目所给五个选项都是正确的。
13.已知函数


正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
12.函数
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
21.设








(1)证明:函数



(2)设有一个与上述等比数列的首项、末项、项数分别相同的等差数列,其各项和为


正确答案
(1)
所以


又

所以


因为




(2)解法一:由题设,
设
当
当
若
若
所以


所以

综上所述,当


解法二 由题设,
当
当

当


假设

那么,当

又
令
所以当



当



所以
故

所以,对于一切

解法三:由已知,记等差数列为




所以
令
当


当
而


若


当


从而




所以当


综上所述,当


解析
解析已在路上飞奔,马上就到!
知识点
9. 定义在





的零点个数为 个
正确答案
4
解析
因为











考查方向
解题思路
判断





易错点
①注意不到
知识点
扫码查看完整答案与解析




























