- 函数与方程
- 共222题
已知定义在







正确答案
解析
略
知识点
对


(1)求证:

(2)若直线






(3)对















正确答案
见解析
解析
(1)由





并且对

(2)由题设及(1)的结论,两个函数图像有且仅有一个公共点,即方程

整理方程得
由

此时方程的两个实数根


得
因为



(3)当


且
① 当







对于函数




此时方程



(16分)
② 当





综上,当





知识点
已知函数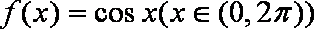
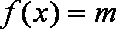
正确答案
解析
设两个根依次为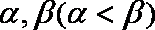
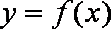
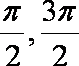
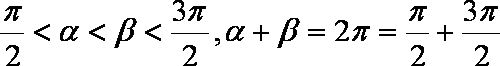
知识点
已知函数

正确答案
解析
略
知识点
已知函数


(1)证明:函数

(2)求方程
(3)若数列




正确答案
见解析。
解析
解:
(1)由




(2)由(1)得:








解法1:


当







(3)记


(i)当







②假设当








(ii)当







①当








故对任意的

综上所述,存在常数


知识点
某同学为研究函数









正确答案

解析
略
知识点
“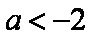
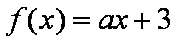
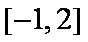
正确答案
解析
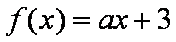
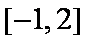
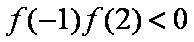
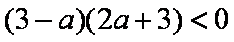
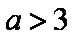
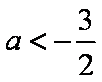
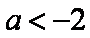
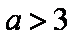
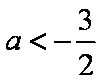
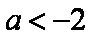
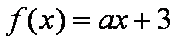
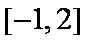
知识点
已知

①


②对任意不同的

那么,关于


正确答案
解析
令
则

又因为









知识点
已知函数







正确答案
解析
略
知识点
5. 下列函数中,在
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析