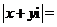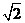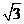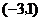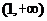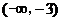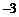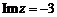- 数系的扩充和复数的引入
- 共917题
2.设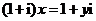
正确答案
知识点
1.已知

正确答案
解析
A
∴


考查方向
解题思路
复数的分类及对应点的位置问题都可以转化为复数的实部与虚部应该满足的条件问题,只需把复数化为代数形式,列出实部和虚部满足的方程(不等式)组即可。
易错点
对复数的几何意义不熟悉导致出错。
知识点
已知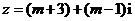
正确答案
知识点
2. 设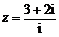
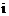
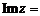
正确答案
解析
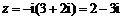
知识点
9.已知


正确答案
2
解析




考查方向
解题思路
本题首先求出实数a,b,然后求比值。首先对于复数的四则运算,要切实掌握其运算技巧和常规思路,如





易错点
相关知识点不熟悉导致出错。
知识点
1.设i是虚数单位,则复数
正确答案
解析
由题意

考查方向
解题思路
先化简,再根据复数的几何意义做判断
易错点
复数的运算错误,复数的几何意义理解的不透彻
知识点
1.已知
正确答案
解析
由题意得,
考查方向
解题思路
直接根据复数的运算法则求解既可。
易错点
在计算上失误丢分。
知识点
2.已知
正确答案
解析

所以
考查方向
解题思路
本题属于简单题,可使用直接法,
(1)化简

(2)观察实部和虚部,使得虚部等于0
易错点
计算过程易忽略
知识点
9.已知复数z=(5+2i)2(i为虚数单位),则z的实部为________.
正确答案
21.
解析
先做乘法运算,z=25+20i-4=21+20i, 实部为21.
考查方向
解题思路
先做乘法运算,注意:
易错点
对复数的乘法运算不熟练,不理解复数的实部.
知识点
2.复数
正确答案
解析
考查方向
解题思路
化成复数一般形式,根据一般形式判断虚数部分
易错点
忽略
知识点
2.已


正确答案
解析
由题意,得

考查方向
解题思路
1)求出复数的共轭复数和
2)求出
易错点
本题易在求复数的虚部时出现错误,易忽视“


知识点
11.设复数a+bi(a,b

正确答案
3
解析
由


所以
考查方向
解题思路
复数的考查核心是代数形式的四则运算,即使是概念的考查也需要相应的运算支持.本题首先根据复数模的定义得


易错点
复数运算的化简计算
知识点
2.设i是虚数单位,则复数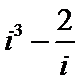
正确答案
解析
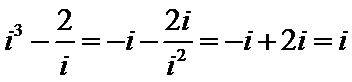
考查方向
解题思路
直接根据复数的运算法则求解既可。
易错点
对于题中的负号处理可能会出错。
知识点
3.定义运算


正确答案
解析


考查方向
解题思路
本题属于简单题,可使用直接法,
(1)化简z得到
(2)观察实部和虚部对应的正负
易错点
计算过程忽视定义的规律出错
知识点
1.若

正确答案
解析
由




因此A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
根据


易错点
化简z时易出错
知识点
扫码查看完整答案与解析