- 直线与平面平行的判定与性质
- 共271题
16.如图,已知直三棱柱ABC—A1B1C1,


(1)判断直线CF和平面AEB1的位置关系,并加以证明;
(2)求四棱锥A—ECBB1的体积.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知圆柱







(1)求曲线
(2)当

(3)是否存在



正确答案
解法一:(1)将圆柱一半展开后底面的半个圆周变成长方形的边BA,曲线




(2)当


故点

连结AP、BP,OP. 由


从而平面


所以,

在


于是:
所以,点

(3)由于二面角


过

由于




于是



若


令




所以



故不存在




解法二:如图,以O为原点,OB所在直线为x轴,过O与OB垂直的直线为y轴,建立空间直角坐标系。
则


所以



(1)同解法一;
(2)当



又


(3)设

取

由

以下同解法一。
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在四棱锥






(1)点



(2)若






正确答案
解法一:(1)因为


因为平面






所以




(2)如图,因为



所以





设面






所以



由平面



解法二:(1)同一
(2)在平面






设平面




由



解得



因为面




所以




解析
解析已在路上飞奔,马上就到!
知识点
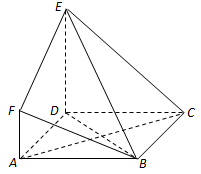
16.如图,
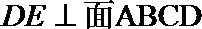
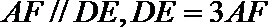
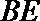
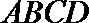
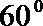
(1)求二面角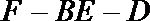
(2)设点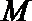
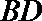
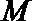
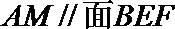
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.能够把圆



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析