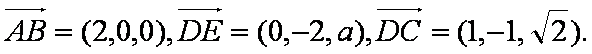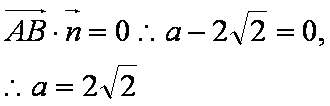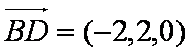- 直线与平面平行的判定与性质
- 共271题
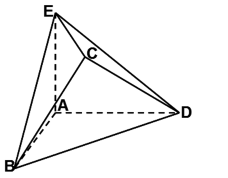
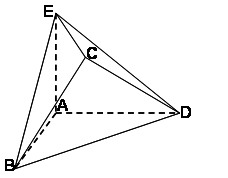
在几何体ABCDE中,AB=AD=BC=CD=2, 
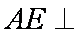
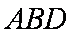
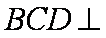
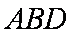
(1)当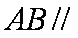
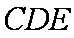
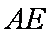
(2)当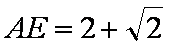
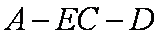
正确答案
见解析
解析
解:(1)设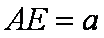
则A(0,0,0),B(2,0,0),D(0,2,0),E(0,0,a),
取BD的中点T,连接CT,AT,则CT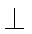
又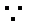
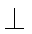
所以CT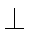
所以CT//AE.
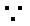

所以CD
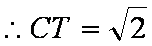
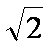
设平面CDE的法向量为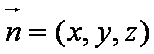
则有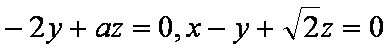
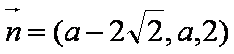
即AE的长为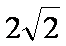
(2)连接AC,当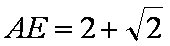
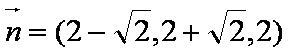
又BD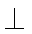
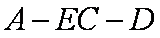
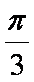
知识点
抛物线


正确答案
解析
对y=x2-4x+3求导可得,y′=2x-4
∴抛物线y=x2-4x+3及其在点A(1,0)和B(3,0)处的两条切线的斜率分别为-2,2
从而可得抛物线y=x2-4x+3及其在点A(1,0)和B(3,0)处的两条切线方程分别为
l1:2x+y-2=0,l2:2x-y-6=0
由
S=

+




知识点
如图,正三棱柱ABC-A1B1C1中,底面边长为2,侧棱长为


(1)求证;

(2)求二面角A1-AB1-D的大小。
正确答案
见解析。
解析
(1)如图,连结A1B与AB1交于E,连结DE,则E为A1B的中点,
∴BC1∥DE,



∴

(2)过D作DF⊥A1B1于F,
由正三棱柱的性质,AA1⊥DF,∴DF⊥平面ABB1A1,
连结EF,DE,在正三角形A1B1C1中,
∵D是A1C1的中点,∴

又在直角三角形AA1D中,
∵
∴DE⊥AB1,∴可得EF⊥AB1,
则∠DEF为二面角A1-AB1-D的平面角,
可求得
∵△B1FE∽△B1AA1,得
∴
(2)解法(二)(空间向量法)
建立如图所示空间直角坐标系,则A(0,-1,0),B1(0,1,
C1(-





∴
设n1=(x,y,z)是平面AB1D的一个法向量,
则可得 

∴
又平面ABB1A1的一个法向量
设n1与n2的夹角是θ,则 cosθ=

又可知二面角A1-AB1-D是锐角。
∴二面角A1-AB1-D的大小是
知识点
已知函数
(1)求
(2)若将


正确答案
(1)
解析
(1)
=
所以

(2)∵将


∴
∵
∴当
当
知识点
为了了解某校高三学生的视力情况,随机抽查了该校100名高三学生的视力情况,得到频率分布直方图如下图,由于不慎将部分数据丢失,但知道后5组频数和为62,设视力在4.6到4.8之间的学生数为a,最大频率为0.32,则a的值为( )
正确答案
解析
前两组中的频数为100×(0.05+0.11)=16.
∵后五组频数和为62,∴前三组频数和为38. ∴第三组频数为22.
又最大频率为0.32,故频数为0.32×100=32,∴a=22+32=54,故选B
知识点
扫码查看完整答案与解析