- 指数函数的单调性与特殊点
- 共400题
1.

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.某化工厂生产一种溶液,按市场要求,杂质含量不能超过0.1%,若最初生产出的溶液含杂质2%,需要进行过滤,且每过滤一次可使杂质含量减少
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若角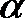
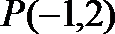
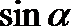
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.

(Ⅰ)求函数f(x)的单调区间;
(Ⅱ) 若当x>0时,f(x)>
正确答案
解:(Ⅰ)f
∵ x > 0 ∴ f
∴f(x)在(0,+
(Ⅱ) 当x > 0时, f(x) > 
既 k < (x+1)
设g(x)= (x+1)


令 g


∴ g(x)在(0,x

∴g(x)
=

由 y = x - 1和y = ln(x+1)的图象可知 2 < x
∴x

解析
解析已在路上飞奔,马上就到!
知识点
7.在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设数列



(1)求数列
(2)若




(3)求

正确答案
解:(1)依题意得,
即
当n≥2时,
当n=1时,a1=S1=2
所以
(2)




(3)


(1)—(2),得




解析
解析已在路上飞奔,马上就到!
知识点
21.已知:



(1)当



(2)若





(3)在(2)的条件下,设



正确答案
(1)

当且仅当




(2)

当且仅当



(3)因为

所以
解析
解析已在路上飞奔,马上就到!
知识点
22.已知二次函数


(1)当0<





(2)如果



(3)令





正确答案
(1) 由




即


(2)由


当


当
对于任意的







⑶ 当


故



故
则数列


又
由①—②得
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析