指数函数的单调性与特殊点
共400题

· 指数函数的单调性与特殊点

指数函数的单调性与特殊点
共400题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

21．设函数．

（1）若函数在处有极值，求函数的最大值；

（2）是否存在实数，使得关于的不等式在上恒成立？

若存在，求出的取值范围；若不存在，说明理由；

（3）记，证明：不等式．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：填空题

填空题 · 4 分

10．函数图像的对称中心是（）

正确答案

解析

因为函数为奇函数，对称中心是，因此函数图像的对称中心是.

知识点

指数函数的单调性与特殊点

题型：单选题

单选题 · 5 分

16．若是的最小值，则的取值范围为（）

A[-1，2]

B[-1，0]

C[1，2]

D[0，2]

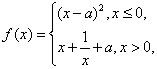
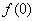
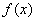
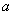
正确答案

解析

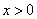
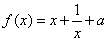
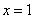
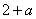
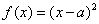
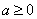
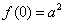
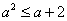
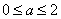
由于当时，在时取得最小值，由题意当时，应该是递减的，则，此时最小值为，因此，解得，选D．

知识点

指数函数的单调性与特殊点

题型：简答题

简答题 · 14 分

21．市场上有一种新型的强力洗衣液，特点是去污速度快。已知每投放a（，且）个单位的洗衣液在一定量水的洗衣机中，它在水中释放的浓度（克/升）随着时间（分钟）变化的函数关系式近似为，其中。若多次投放，则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和。根据经验，当水中洗衣液的浓度不低于4（克/升）时，它才能起到有效去污的作用。

　　（1）若只投放一次4个单位的洗衣液，则有效去污时间可达几分钟？

　　（2）若第一次投放2个单位的洗衣液，6分钟后再投放个单位的洗衣液，要使接下来的4分钟中能够持续有效去污，试求的最小值（按四舍五入精确到）。

正确答案

解：（1）因为，所以。

则当时，由，解得，所以此时。

当时，由，解得，所以此时。

综上，得，若一次投放4个单位的洗衣液，则有效去污时间可达8分钟。

（2）当时，，

当且仅当时等号取到。（因为，所以能取到）所以y有最小值。

令，解得，

所以的最小值为。

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：填空题

填空题 · 4 分

9．已知，则的值为_______

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：填空题

填空题 · 4 分

5．同时满足（1）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：填空题

填空题 · 4 分

8．方程有解，则________

正确答案

[-3,1]

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：填空题

填空题 · 4 分

11．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：填空题

填空题 · 4 分

13．已知。若，则的取值范围为__________。

正确答案

解析

由已知得，，所以。因为，所以（因为等号仅当时取到，与a．b为底数矛盾），所以，所以。

知识点

指数函数的单调性与特殊点

题型：填空题

填空题 · 4 分

3．三角形的三边之比为,则此三角形的最大内角是____

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

继续学习学习下一知识点

下一知识点 : 指数函数单调性的应用

百度题库 > 高考 > 理科数学 > 指数函数的单调性与特殊点

扫码查看完整答案与解析