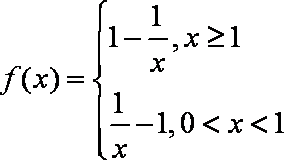
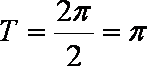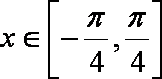- 指数函数的单调性与特殊点
- 共400题
定义在(—1, 1)上的函数f(x)满足:




正确答案
解析
∵函数f(x)满足:


令

∴



∵
∴



知识点
若函数





正确答案
②③
解析
在①中,若














知识点
某商场在庆元宵促销活动中,对元宵节9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售额为_____万元.
正确答案
10
解析
知识点
某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试. 假设某学生每次通过测试的概率都是
(1)求该学生考上大学的概率.
(2)如果考上大学或参加完5次测试就结束,记该生参加测试的次数为ξ,求变量ξ的分布列及数学期望Eξ。
正确答案
见解析
解析
解析:(1)记“该生考上大学”的事件为事件A,其对立事件为
∴
(2)该生参加测试次数ξ的可能取值为2,3,4,5.




知识点
如题(19)图,直三棱柱ABC—A1B1C1中,∠ACB=90°,AA1=3,
AC=2,D为AB中点,E为BB1上一点,
(1)当
(2)若直线CE 与平面


正确答案
解析
(1)建立空间直角坐标系如图所示,则



又


(2)由题知





即
解得
知识点
已知函数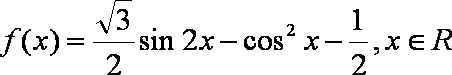
(1)求函数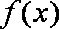
(2)求函数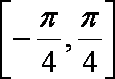
正确答案
(1)最小值是-2,最小正周期是是
(2)最大值为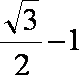
解析
解析:(1)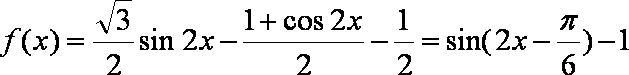
则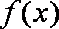
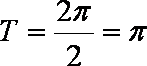
(2)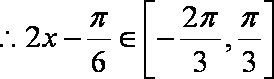
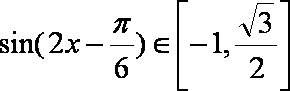
所以最大值为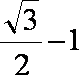
知识点
在我校第十六届科艺读书节活动中,某班50名学生参加智力答题活动,每人回答3个问题,答对题目个数及对应人数统计结果见下表:
根据上表信息解答以下问题:
(1)从50名学生中任选两人,求两人答对题目个数之和为4或5的概率;
(2)从50名学生中任选两人,用

正确答案
见解析
解析
解析(1)记“两人答对题目个数之和为4或5”为事件A,则

即两人答对题目个数之和为4或5的概率为
(2)依题意可知X的可能取值分别为0,1,2,3.
则



从而X的分布列为:
X的数学期望
知识点
对任意的实数x,y,定义运算
正确答案
解析
所以












故选:A
知识点
已知函数
(1)当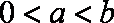
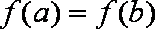
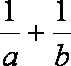
(2)是否存在实数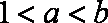

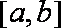
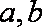
正确答案
(1)2(2)不存在
解析
(1)因为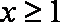


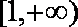
因为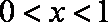
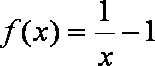
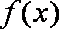
所以当
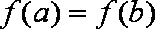

所以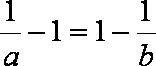
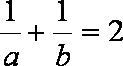
(2)不存在. 因为当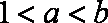
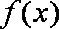
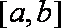
所以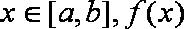
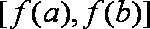
而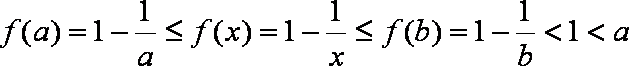
所以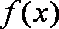
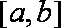
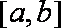
故不存在实数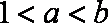
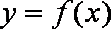
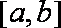
知识点
已知向量


(1)求
(2)作出函数

(3)在




正确答案
见解析
解析
(1)f(x)=
=cos2wx+sin2wx+1=2sin(2wx+
由题意知T=π,又T=
(2)图省略
(3)f(x)=2sin(2x+
∴f(A)=2sin(2A+


∵0<A<π, ∴


∴2A+

∴S△ABC=

∴a2=b2+c2-2bccosA=1+4-2×2×1×=3
∴a=
知识点
扫码查看完整答案与解析