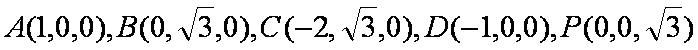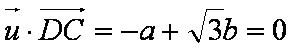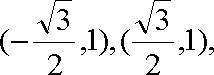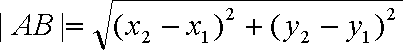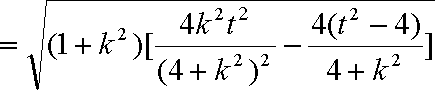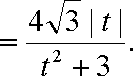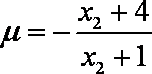- 指数函数的单调性与特殊点
- 共400题
已知函数
(1)当

(2)当函数


正确答案
见解析
解析
解(1)当


所以定义域为

(2)设函数



由绝对值三角不等式
所以

知识点
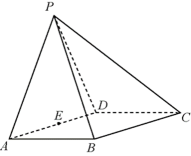
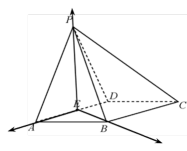
如图所示,在四棱锥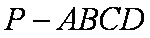
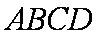
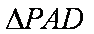
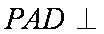
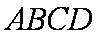
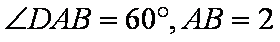
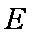
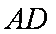
(1)求证: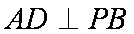
(2)在棱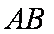
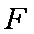
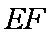
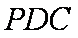
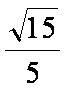
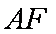
正确答案
见解析
解析
解(1)证明:连接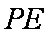
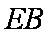
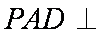
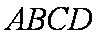
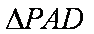
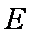
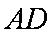
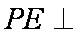
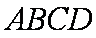

因为四边形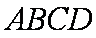
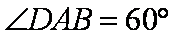
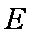
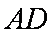
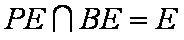
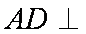
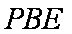
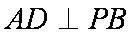
(2)
以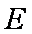
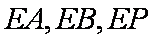
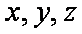
因为点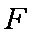
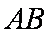
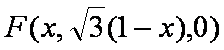
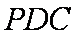
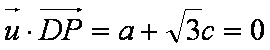
所以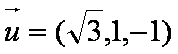

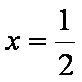
所以存在点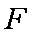
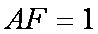
知识点
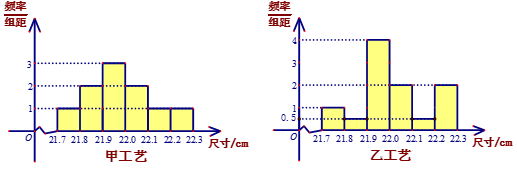
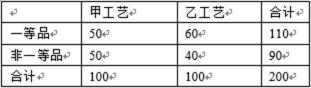
某工厂用甲、乙两种不同工艺生产一大批同一种零件,零件尺寸均在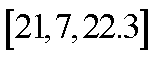
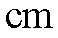
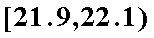


(1) 根据上述数据完成下列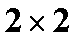
附:
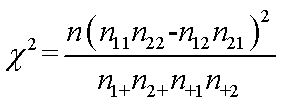
(2)以上述各种产品的频率作为各种产品发生的概率,若一等品、二等品、三等品的单件利润分别为30元、20元、15元,你认为以后该工厂应该选择哪种工艺生产该种零件?请说明理由。
正确答案
见解析。
解析
(1)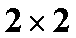
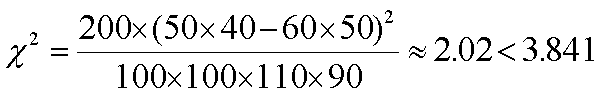
由题知运用甲工艺生产单件产品的利润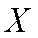
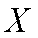
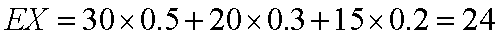
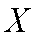
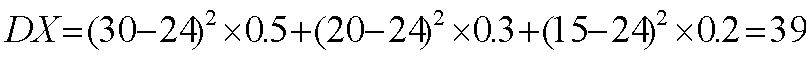
乙工艺生产单件产品的利润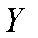
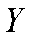
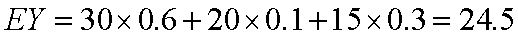
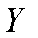
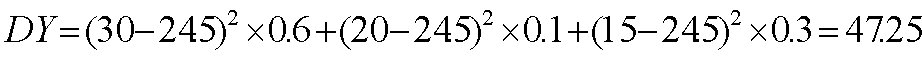
回答一:由上述结果可以看出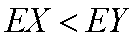
回答二:由上述结果可以看出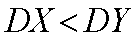
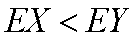
知识点
已知



正确答案
解析
略
知识点
已知

①将

②将①中的图象的纵坐标不变,横坐标缩短为原来的
③将②中的图象的横坐标不变,纵坐标伸长为原来的2倍。
(1)求
(2)在



正确答案
见解析。
解析
(1)由变换得
所以
由

(2)由



在


联立

知识点
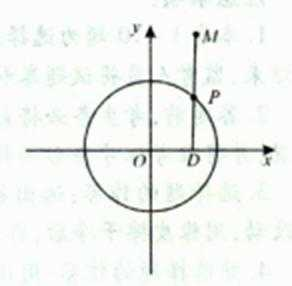
如图,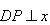

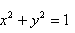
(1)求点M的轨迹C的方程;
(2)过点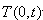
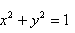
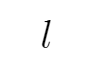
正确答案
见解析
解析
设点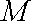
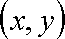
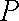
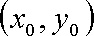
则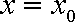
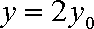
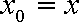
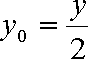
因为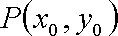
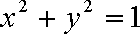
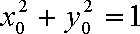
将①代入②,得点
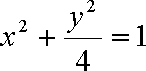
(2)由题意知,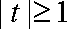
当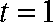
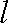
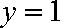
此时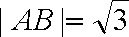
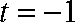
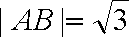
当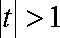
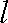
由
得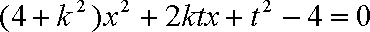
设A、B两点的坐标分别为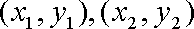
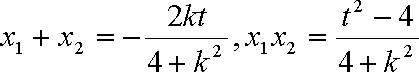
又由l与圆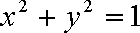
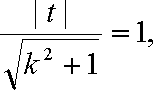
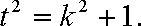
所以
因为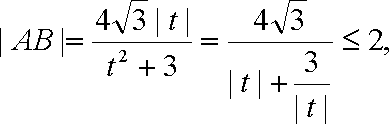
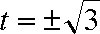
依题意,圆心
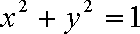
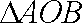
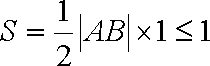
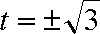
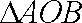

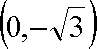
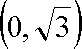
知识点
已知
① 


正确答案
解析
由平面向量的基础知识可知①②④均不正确,只有③正确,故选A.
知识点
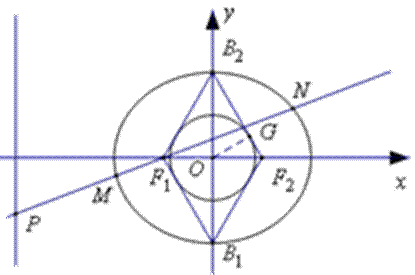
如图,椭圆C:

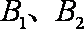

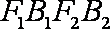
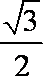
(1) 求椭圆C的方程;
(2)过左焦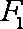
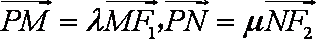
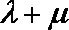
正确答案
见解析。
解析
(1)如图所示,设四边形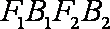
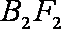
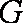
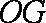
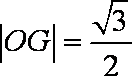
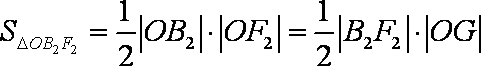
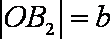

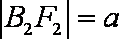
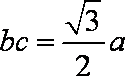
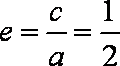
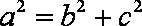
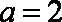
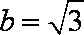
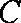
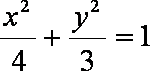
(2)根据已知条件可设直线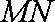
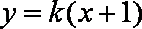
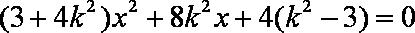
设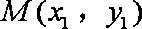
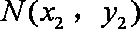
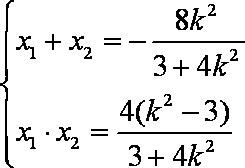
又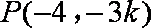
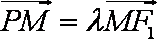
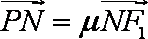
得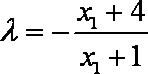
∴ 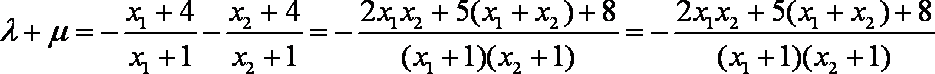
∵
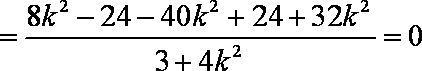
∴ 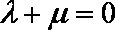
知识点
利用如图所示程序框图在直角坐标平面上打印一系列点,则打印的点落在坐标轴上的个数是
正确答案
解析
i=3,打印点(-2,6),x=-1,y=5,
i=3-1=2;i=2,打印点(-1,5),x=0,y=4,
i=2-1=1;i=1,打印点(0,4),x=1,y=3,
i=1-1=0;0不大于0,所以结束,故选B.
知识点
12.(x2+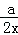
正确答案
解析
略。
知识点
扫码查看完整答案与解析