- 指数函数的单调性与特殊点
- 共400题
21.设函数

(1)若


(2)如果

(3)是否存在最小的正整数


正确答案
(1)由题意知,


由


当



所以当



∴ 
(2)由题意

即

设
又对称轴
则

(3)对于函数

则

所以函数

又

即


显然,存在最小的正整数


解析
解析已在路上飞奔,马上就到!
知识点
18.某公司计划在迎春节联欢会中设一项抽奖活动:在一个不透明的口袋中装入外形一样号码分别为1,2,3,…,10的十个小球。活动者一次从中摸出三个小球,三球号码有且仅有两个连号的为三等奖,奖金30元;三球号码都连号为二等奖,奖金60元;三球号码分别为1,5,10为一等奖,奖金240元;其余情况无奖金。
(1)求员工甲抽奖一次所得奖金ξ的分布列与期望;
(2)员工乙幸运地先后获得四次抽奖机会,他得奖次数
正确答案
(1)甲抽奖一次,基本事件总数为
一等奖的情况只有一种,所以奖金为240元的概率为P(ξ=240)=
三球连号的情况有1,2,3;2,3,4;……8,9,10共8种,所以P(ξ=60)=
仅有两球连号中,对应1,2与9,10的各有7种;对应2,3;3,4;……8,9各有6种。
得奖金30的概率为P(ξ=30)=
奖金为0的概率为P(ξ=0)=
ξ的分布列为:
(2) 由(1)可得乙一次抽奖中中奖的概率为P=
四次抽奖是相互独立的, 所以中奖次数η~B(4,

解析
解析已在路上飞奔,马上就到!
知识点
5.如图,函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.函数f(x)=ln x-
(1)当a=-2时,求f(x)的最小值;
(2)若f(x)在[1,e]上的最小值为,求a的值。
正确答案
(1)当a=-2时,f(x)=
当x∈(0,2)时,f′(x)<0,当x∈(2,+∞)时,f′(x)>0,
∴f(x)在(0,2)上为减函数,在(2,+∞)上为增函数.
∴f(x)min=f(2)=ln 2+1.
(2)f′(x)=
①当a≥-1时,对任意x∈[1,e],
f′(x)≥0,此时f(x)在[1,e]上为增函数,∴f(x)min=f(1)=-a=
∴a=
②当a≤-e时,对任意x∈[1,e],
f′(x)≤0,此时f(x)在[1,e]上为减函数.∴f(x)min=f(e)=1-

∴a=
③当-e<a<-1时,令f′(x)=0,得x=-a,当1<x<-a时,f′(x)<0,
f(x)在(1,-a)上递减.同理,f(x)在(-a,e)上递增.∴f(x)min=f(-a)=ln(-a)+1=
∴a=-

解析
解析已在路上飞奔,马上就到!
知识点
20.设函数f(x)=x2+bln(x+1),其中b≠0
(1)如果函数f(x)在定义域内既有极大值又有极小值,求实数b的取值范围;
(2)求证对任意的n∈N*不等式ln(

正确答案
(1)由题意f′(x)=2x+

即2x2+2x+b=0在(-1,+∞)有两个不等实根,
设g(x)=2x2+2x+b,则
△=4−8b>0且g(−1)>0,
0<b<
(2)对于函数f(x)=x2-ln(x+1),令函数h(x)=x3-f(x)=x3-x2+ln(x+1)
则h′(x)=3x2−2x+

当x∈[0,+∞)时,h'(x)>0,
所以函数h(x)在[0,+∞)上单调递增,
又h(0)=0,∴x∈(0,+∞)时,恒有h(x)>h(0)=0
即x2<x3+ln(x+1)恒成立.取x=
则有ln(

解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数
(1)求
(2)若

正确答案
(2)
解析
解析已在路上飞奔,马上就到!
知识点
20.设椭圆E中心在原点,焦点在x轴上,短轴长为4,点Q(2,
(1)求椭圆E的方程;
(2)设动直线L交椭圆E于A、B两点,且
(3)过M(







正确答案
解:(1)因为椭圆E: 

故可求得b=2,a=2
(2)设P(x,y),A(x1,y1),B(x2,y2),当直线L斜率存在时设方程为
解方程组


则△=
即

要使


所以

将它代入()式可得
P到L的距离为
又
将
① 当
由
② 当
③ 当AB的斜率不存在时, 
(3)点P(





故点M(


故直线MN的方程,
设G,H分别是直线MN与椭圆准线,
由


由


故
又P(
有


解析
解析已在路上飞奔,马上就到!
知识点
7.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若实数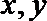
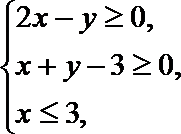
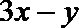
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
13.当x∈(1,2)时,不等式(x-1)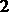
正确答案
{a|1<a≤2}
解析
设y=(x-1)2,y=logax.在同一坐标系中作出它们的图象,如图所示.
若0<a<1,则当x∈(1,2)时,(x-1)2<logax是不可能的,所以a应满足
解得1<a≤2.所以,a的取值范围为{a|1<a≤2}.
知识点
扫码查看完整答案与解析