- 指数函数的单调性与特殊点
- 共400题
20. 已知△ABC中, 点A,B的坐标分别为(-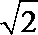
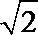
(1)若点C坐标为(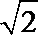
(2)过点P(m,0)作倾斜角为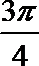
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.过椭圆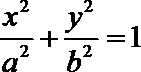
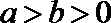
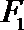
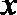
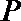
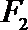
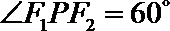
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.由等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数





(Ⅰ)求
(Ⅱ)求
(Ⅲ)设




正确答案
解:(Ⅰ)

(Ⅱ)此时


所以



当



当 



所以,增区间为(0,1) 减区间为(1,
(Ⅲ)


记



当



当



所以,

记




所以,

综①、②知,
解析
解析已在路上飞奔,马上就到!
知识点
10.若在区域

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知各项均为正数的等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,从A1(1,0,0),A2(2,0,0),B1(0,1,0,)B2(0,2,0),C1(0,0,1),C2(0,0,2)这6个点中随机选取3个点。
(1)求这3点与原点O恰好是正三棱锥的四个顶点的概率;
(2)求这3点与原点O共面的概率。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请在第22、23、24题中任选一道作答.
22.选修4-1:几何证明选讲
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交于BC于点E,AB=2AC.
(1)求证:BE=2AD;
(2)当AC=1,EC=2时,求AD的长.
23.选修4-4:坐标系与参数方程
已知在直角坐标系xOy中,圆锥曲线C的参数方程为

(1)写出直线l的参数方程和圆的标准方程;
(2)设直线l与圆相交于A,B两点,求|PA|·|PB|的值.
24.选修4-5:不等式选讲
设f(x)=|x+1|+|x-3|.
(1)解不等式f(x)≤3x+4;
(2)若不等式f(x)≥m的解集为R,求实数m的取值范围.
正确答案
22.
23.
24.
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析