- 简单复合函数的导数
- 共526题
1
题型:
单选题
|

正确答案
D
解析
本题考查了定积分的运算。
知识点
简单复合函数的导数
1
题型:
单选题
|
已知集合

正确答案
C
解析
略。
知识点
简单复合函数的导数
1
题型:填空题
|
在区间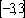

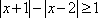
正确答案
解析
略。
知识点
简单复合函数的导数
1
题型:简答题
|
若函数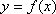
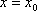

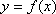
已知
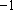
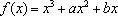
(1)求
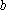
(2)设函数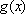
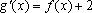
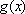
(3)设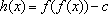
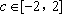
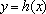
正确答案
见解析
解析
(1)由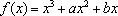
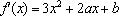
∵1和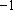

∴ 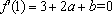
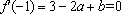
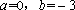
(2)∵ 由(1)得,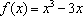
∴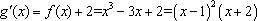
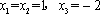
∵当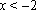
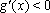
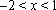
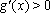
∴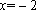
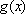
∵当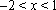
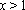
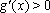
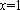

∴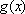
(3)令
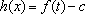
先讨论关于
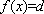
当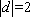

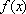
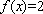
当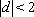
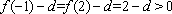
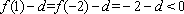
∴一2 , -1,1 ,2 都不是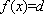
由(1)知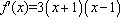
① 当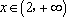

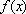
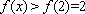
此时
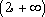
② 当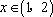

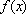
又∵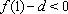
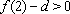
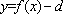
∴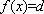
同理,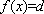
③ 当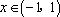
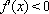
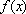
又∵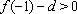
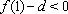
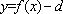
∴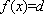
因此,当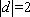
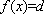


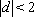
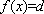
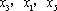
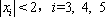
现考虑函数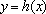
( i )当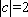
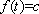
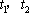
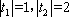
而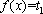
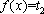
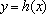
( 11 )当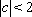
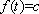
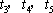
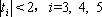
而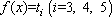
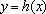
综上所述,当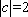
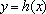
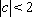
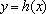
知识点
简单复合函数的导数
1
题型:
单选题
|
设变量x,y满足

正确答案
D
解析
画出可行域,根据图形可知当x=5,y=15时2x+3y最大,最大值为55,故选D
知识点
简单复合函数的导数
下一知识点 : 定积分
扫码查看完整答案与解析