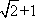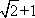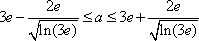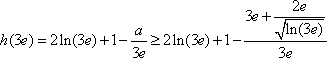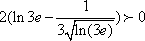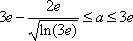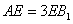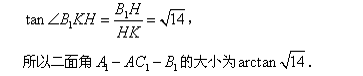- 简单复合函数的导数
- 共526题
已知正方形ABCD的边长为2,E为CD的中点,则
正确答案
2
解析
以AB所在直线为x轴,AD所在直线为y轴建立平面直角坐标系,如图所示,则点A的坐标为(0,0),点B的坐标为(2,0),点D的坐标为(0,2),点E的坐标为(1,2),则

知识点
设二项式

正确答案
2
解析
由题意得
∴


∴



知识点
△ABC的内角A,B,C的对边分别为a,b,c,已知a=bcos C+csin B.
(1)求B;
(2)若b=2,求△ABC面积的最大值。
正确答案
(1) 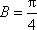
解析
(1)由已知及正弦定理得
sin A=sin Bcos C+sin Csin B,①
又A=π-(B+C),故
sin A=sin(B+C)=sin Bcos C+cos Bsin C,②
由①,②和C∈(0,π)得sin B=cos B,
又B∈(0,π),所以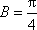
(2)△ABC的面积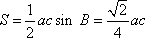
由已知及余弦定理得4=a2+c2-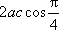
又a2+c2≥2ac,故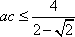
因此△ABC面积的最大值为
知识点
设函数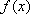


(1)若

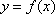

(2)求实数


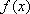
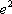
注:
正确答案
(1)
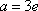
解析
(1)解:求导得f’(x)=2(x-a)lnx+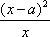


因为x=e是f(x)的极值点,所以f’(e)= 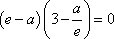
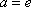
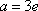
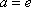
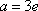
(2)解:①当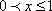
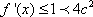
②当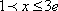
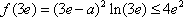
解得
由(Ⅰ)知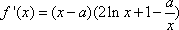
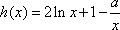
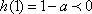
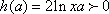
且
=
又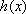
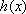
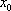

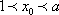
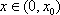
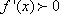
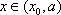
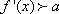
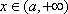
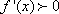
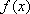
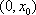
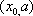
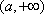

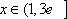
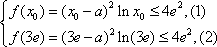
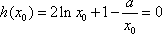
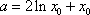
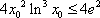
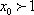
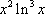
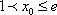
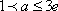
由(2)解得,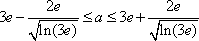
综上,a的取值范围为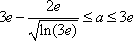
知识点
一个盒子装有六张卡片,上面分别写着如下六个函数:





(1)从中任意拿取
(2)现从盒子中逐一抽取卡片,且每次取出后均不放回,若取到一张写有偶函数的卡片则停止抽取,否则继续进行,求抽取次数
正确答案
见解析。
解析
(1)





所有的基本事件包括两类:一类为两张卡片上写的函数均为奇函数;
另一类为两张卡片上写的函数为一个是奇函数,
一个为偶函数;故基本事件总数为
满足条件的基本事件为两张卡片上写的函数均为奇函数,故满足条件的基本事件个数为
故所求概率为
(2)


故


知识点







正确答案
见解析。
解析
由
由已知得
从而

由正弦定理得

所以

知识点
若曲线


正确答案
解析
略
知识点
已知抛物线









正确答案
2
解析
略
知识点
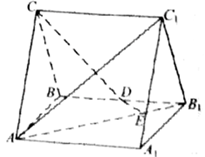
如图,直三棱柱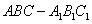
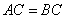
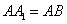
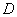
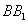
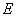
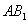
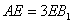
(1)证明: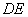
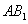
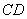
(2)设异面直线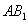
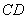
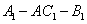
正确答案
见解析。
解析
解法一:(1)连接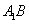
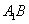
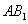
因为面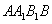
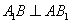
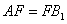
又

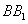
故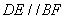
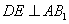
作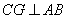
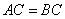
又由底面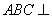
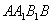

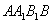
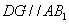
故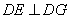
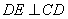
所以DE为异面直线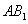
(2)因为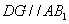
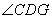
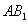
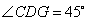
设
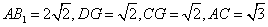
作
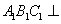
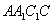
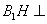
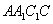
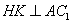
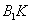

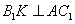
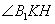
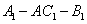
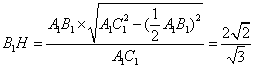
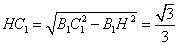
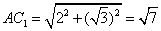
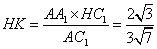
解法二:
(1)
(2)因为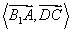
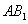
故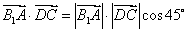
即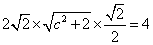
解得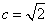
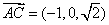
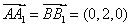
所以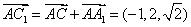
设平面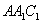
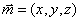
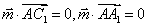
即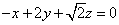
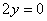
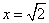
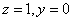
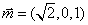
设平面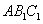
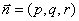

即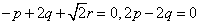
令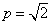
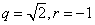
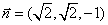
所以
由于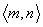

所以二面角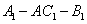
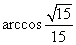
知识点
设函数
(1)证明:当

(2)设当

正确答案
见解析。
解析
(1)
于是




所以当

(2)由题设

当



源头学子 http://www.wxckt.cn 特级教师王新敞 wxckt@126.com
知识点
扫码查看完整答案与解析