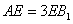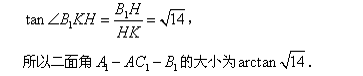- 简单复合函数的导数
- 共526题
1
题型:简答题
|







正确答案
见解析。
解析
由
由已知得
从而

由正弦定理得

所以

知识点
简单复合函数的导数
1
题型:
单选题
|
若曲线


正确答案
A
解析
略
知识点
简单复合函数的导数
1
题型:填空题
|
已知抛物线









正确答案
2
解析
略
知识点
简单复合函数的导数
1
题型:简答题
|
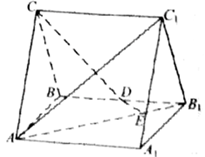
如图,直三棱柱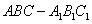
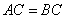
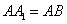
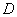
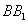
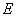
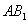
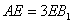
(1)证明: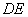
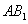
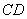
(2)设异面直线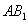
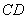
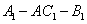
正确答案
见解析。
解析
解法一:(1)连接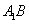
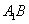
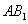
因为面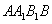
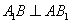
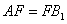
又

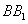
故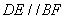
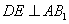
作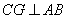
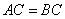
又由底面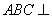
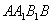

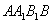
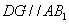
故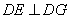
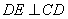
所以DE为异面直线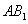
(2)因为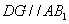
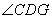
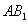
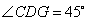
设
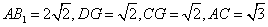
作
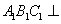
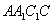
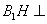
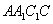
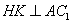
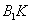

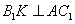
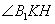
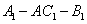
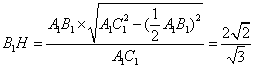
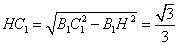
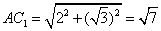
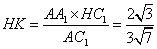
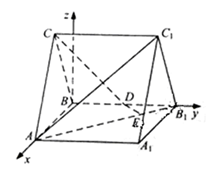
解法二:
(1)
(2)因为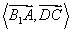
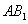
故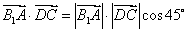
即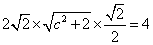
解得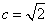
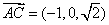
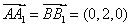
所以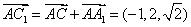
设平面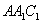
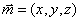
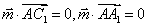
即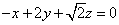
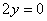
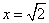
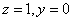
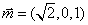
设平面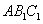
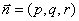

即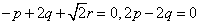
令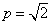
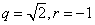
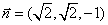
所以
由于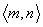

所以二面角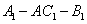
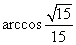
知识点
简单复合函数的导数
1
题型:简答题
|
设函数
(1)证明:当

(2)设当

正确答案
见解析。
解析
(1)
于是




所以当

(2)由题设

当



源头学子 http://www.wxckt.cn 特级教师王新敞 wxckt@126.com
知识点
简单复合函数的导数
下一知识点 : 定积分
扫码查看完整答案与解析