- 简单复合函数的导数
- 共526题
20.甲、乙两地相距



(1)将全程运输成本

(2)为了使全程运输成本最小,货车应以多大的速度行驶.
正确答案
(1)
(2)




当且仅当


当
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆




(1)过F的直线与抛物线



(2)从圆O:


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 设三位数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知数列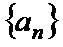

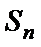

(I)求数列
(II)设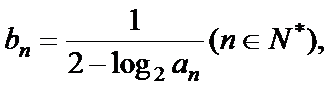



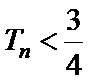
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.
已知椭圆




(Ⅱ)设过点P(-2,0)的直线与椭圆E交于A、B两点,且满足
(1)若

(2) 若M、N分别为椭圆E的左、右顶点,
证明:
正确答案
(Ⅰ)因为焦点为

取椭圆的右焦点



所以椭圆E的方程为



显然直线

由








解得
(2)若


将




解析
解析已在路上飞奔,马上就到!
知识点
5.“


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.把函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 数列




(Ⅰ)求数列
(Ⅱ)设




正确答案
解:(Ⅰ)由已知:对于

∴
①-②得
∴
∵

∴数列
又n=1时,

∴

(Ⅱ) 解:由(1)可知
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数f(x)=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 等比数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析































