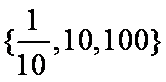直线与双曲线的位置关系
共36题

· 直线与双曲线的位置关系

直线与双曲线的位置关系
共36题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

抛物线（＞）的焦点为，已知点，为抛物线上的两个动点，且满足.过弦的中点作抛物线准线的垂线，垂足为，则的最大值为（）

正确答案

解析

略

知识点

抛物线的标准方程和几何性质直线与双曲线的位置关系

题型：填空题

填空题 · 5 分

二项式（1+sinx）n的展开式中，末尾两项的系数之和为7，且系数最大的一项的值为，则x在[0，2]内的值为。

正确答案

解析

略。

知识点

直线与双曲线的位置关系

题型：简答题

简答题 · 13 分

已知椭圆的一个焦点为，且离心率为，

（1）求椭圆方程；

（2）斜率为的直线过点，且与椭圆交于两点，为直线上的一点，若△为等边三角形，求直线的方程.

正确答案

（1）椭圆方程为

（2）直线的方程为，或

解析

（1）依题意有，，可得，。

故椭圆方程为， ………………………………………………５分

（2）直线的方程为。

联立方程组消去并整理得。

设，，故，。

则。

设的中点为，可得，。

直线的斜率为，又，

所以。

当△为正三角形时，，

可得，解得，

即直线的方程为，或，………………………………13分

知识点

直线与双曲线的位置关系

题型：填空题

填空题 · 5 分

已知实数m>0，定点A（-m，0），B(m，0)，s为一动点，直线SA与直线SB的斜率之积

为

（1）求动点s的轨迹C的方程，并指出它是哪一种曲线；

（2）当时，问t取何值时，直线l：2x-y+t=O (t∈R)与曲线C有且只有一个交点？

正确答案

见解析。

解析

（1）设S(x，y)，则

由题意得即

当O<m<1时，轨迹C是中心在坐标原点，焦点在y轴上的椭圆（除去椭圆与x轴的两个交点）；

当m>l时，轨迹C是中心在坐标原点，焦点在，轴上的椭圆（除去椭圆与x轴的两个交点）：

当m=l时，轨迹C是以原点为圆心，半径为l的圆（除去圆与x轴的两个交点）。

（2）当时，曲线C的方程为

由消去y得

①令得t＝±3。

此时直线l与曲线C有且只有一个公共点，

②令△>0且直线2x-y+1=O恰好过点(，0)时，

此时直线与曲线C有且只有一个公共点，

综上所述，当t=±3或时，直线l与曲线C有且只有一个公共点，

知识点

直线与双曲线的位置关系直接法求轨迹方程

题型：单选题

单选题 · 5 分

已知集合,,那么如图所示的阴影部分表示的集合是( )

B{-1,0,1,2}

D{-1,0,2}

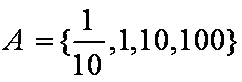
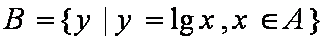
正确答案

解析

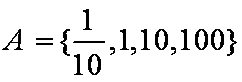
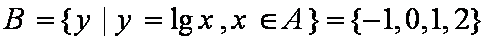
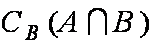
因为,所以，又因为图示的阴影部分是求，所以可得所求的集合为{-1,0,2}.故选D.

知识点

直线与双曲线的位置关系

继续学习学习下一知识点

下一知识点 : 直线与抛物线的位置关系

百度题库 > 高考 > 理科数学 > 直线与双曲线的位置关系

扫码查看完整答案与解析