- 三角函数的周期性及其求法
- 共131题
设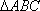
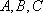
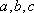
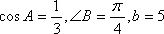
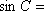
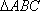
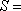
正确答案
解析
略
知识点
已知
(1)求
(2)当

正确答案
(1)
解析
(1)
=
=
=
∴ 
(2) ∵
∴ 
当


当


∴当

知识点
已知函数
(1)求f(x)的最小正周期;
(2)设
正确答案
见解析。
解析
知识点
在极坐标系中,定点




正确答案
解析
略
知识点
在△









(1)当



(2)若

正确答案
(1)
解析
(1)由正弦定理得,

又


(2)由余弦定理,
即
所以
由


由题意知

知识点
已知方程
正确答案
解析

要使方程
则y=|sinx|的图象与直线y=kx(k>0)有且仅有三个公共点,
所以直线y=kx与y=|sinx|在
由

故选C。
知识点
函数
正确答案
解析
略
知识点
由曲线

正确答案
解析
略
知识点
在三棱锥P﹣ABC中,侧梭长均为4.底边AC=4.AB=2,BC=2
(1)求证:平面PAC⊥平面ABC。
(2)求三棱锥P﹣ABC的体积;
(3)求二面角C﹣AD﹣E的余弦值。
正确答案
见解析。
解析
证明:(1)∵PA=PB=PC=AC=4,
取AC的中点O,连接OP,OB,可得:OP⊥AC,

∵
∴OB=OC=2,PB2=OB2+OP2,∴OP⊥OB。
又∵AC∩BO=O且AC、OB⊂面ABC,∴OP⊥平面ABC,
又∵OP⊂平面PAC,∴平面PAC⊥平面ABC,)
(2)由(1)可知:OP⊥平面ABC,∴OP为三棱锥P﹣ABC的高,且OP=
直角三角形ABC的面积S=
∴VP﹣ABC=

(3)方法一:过点E 作EH⊥AC于H,过点H作HM⊥AD于M,
连接ME,∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,EH⊥AC,EH⊂平面ABC,
∴EH⊥平面PAC,∴ME⊥AD(三垂线定理),
∴∠EMH即为所求的二面角的平面角。
∵E,D分别为中点,EH⊥AC,
∴在RT△HEC中:

∴
在RT△HMA中,
在RT△HME中,
所以
方法二:
以O为原点,建立如图所示的空间直角坐标系,
O(0,0,0),A(0,﹣2,0),



∴

设平面AED的一个法向量为
平面ACD的一个法向量为
则



∴
设所求的二面角为θ,显然θ为锐角,




知识点
设向量



正确答案
解析
知识点
扫码查看完整答案与解析