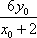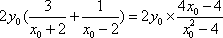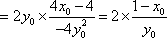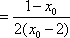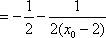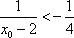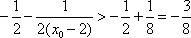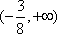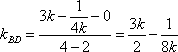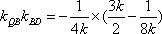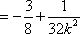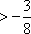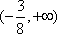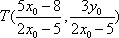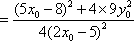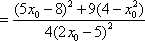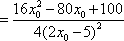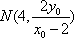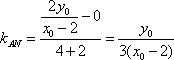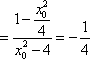- 直接法求轨迹方程
- 共41题
已知点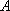
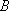

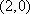
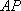
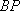


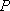
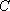
(1)求曲线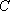
(2)设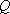
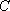
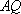
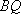
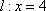
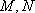
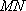
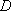

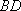
(3)在(2)的条件下,记直线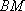
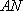
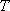

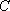
正确答案
见解析。
解析
(1)设动点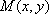
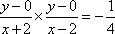

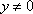
所以曲线
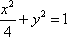
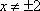
(2)法一:设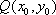

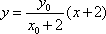
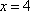
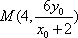
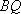
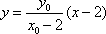
令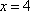
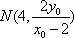
∵ 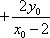
∴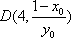
故
∵ 

∴,
∴
∴直线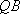

法二:设直线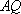
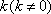
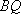
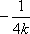
所以直线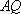
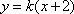
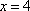
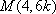
直线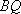
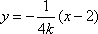
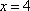
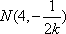
∴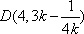
∴
故
∴直线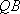
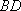
(3)法一:由(2)得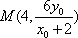
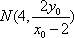
则直线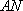
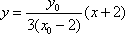
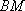
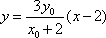
由

∴
∴ 点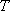

法二:由(2)得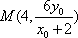
∴ 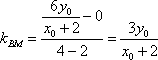
∴
∴ 点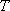
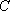
法三:由(2)得,
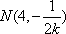
∴ 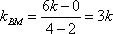
∴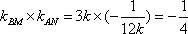


知识点
已知定点




(1)求点

(2)若曲线







正确答案
见解析。
解析
(1)由

根据椭圆定义知

其长轴




(2)过点




相切得
由
联立


直线




令

考查函数


所以



知识点
已知点






(1)求曲线
(2)斜率为








(3)试问:是否存在一个定圆


正确答案
见解析
解析
(1)由题知,有
化简,得曲线

(2)∵直线


∴可设直线

联立方程组

又交点为
∴
∴
(3)答:一定存在满足题意的定圆
理由:∵动圆

∴两圆的圆心之间距离
又



记曲线


∴若定圆的圆心


∴定圆

知识点
在平面直角坐标系中,动点



(1)给出下列三个结论:
①曲线
②曲线

③曲线



其中,所有正确结论的序号是_____;
(2)曲线
正确答案
②③;
解析
略
知识点
曲线



正确答案
1
解析







知识点
扫码查看完整答案与解析