- 直接法求轨迹方程
- 共41题
已知椭圆

(1)求椭圆C1的方程;
(2)设椭圆C1的左焦点为F1,右焦点为F2,直线l1过点F1且垂直于椭圆的长轴,动直线l2垂直于直线l1,垂足为点P,线段PF2的垂直平分线交l2于点M,求点M的轨迹C2的方程;
(3)设C2与x轴交于点Q,不同的两点R,S在C2上,且满足

正确答案
见解析。
解析
(1)由
得


(2)由MP=MF2得动点M的轨迹是以l1:x=﹣1为准线,
F2为焦点的抛物线,∴点M的轨迹C2的方程为y2=4x,
(3)Q(0,0),设
∴
由

∴化简得
∴
∵
又∵y22≥64,∴当y22=64,即y2=±8时
∴
知识点
已知定点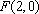
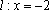
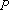

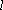
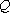
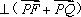

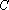
(1)求曲线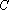
(2)过点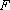
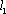

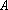
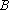
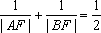
(3)记
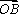
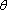

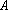
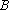
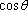
正确答案
见解析
解析
(1)设点

由题意,可得
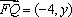
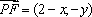
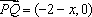
由

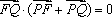
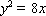
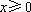
因此,所求曲线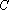
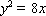
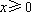
(2)因为过点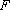


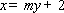
于是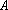
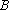
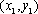
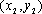
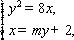
消
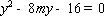
于是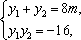

又因为曲线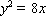
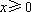

所以
(3)由(2)可知,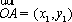
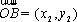
于是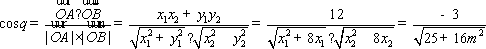
(16分)可求得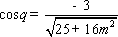
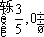
知识点
在平面直角坐标系中,





(1)求曲线
(2)若过点




(3)若曲线




正确答案
见解析
解析
(1)依题意知,动点




以原点为顶点,
∵
∴
∴ 曲线

(2)当




此时
当


则由
设


∴

(3)设
∴
∵
∴
∵
∴
当且仅当 
∵
∴当

知识点
已知两点






(1) 求动点

(2)过点








正确答案
见解析
解析
(1)依据题意,有
∵
∴
∴动点P所在曲线C的轨迹方程是
(2)因直线


故有


设两曲线的交点为


又


于是,可得点

若线段





联立方程组



因此,可算得

所以,四点


知识点
已知实数m>0,定点A(-m,0),B(m,0),s为一动点,直线SA与直线SB的斜率之积
为
(1)求动点s的轨迹C的方程,并指出它是哪一种曲线;
(2)当
正确答案
见解析。
解析
(1)设S(x,y),则
由题意得
当O<m<1时,轨迹C是中心在坐标原点,焦点在y轴上的椭圆(除去椭圆与x轴的两个交点);
当m>l时,轨迹C是中心在坐标原点,焦点在,轴上的椭圆(除去椭圆与x轴的两个交点):
当m=l时,轨迹C是以原点为圆心,半径为l的圆(除去圆与x轴的两个交点)。
(2)当
由
①令
此时直线l与曲线C有且只有一个公共点,
②令△>0且直线2x-y+1=O恰好过点(
此时直线与曲线C有且只有一个公共点,
综上所述,当t=±3或
知识点
扫码查看完整答案与解析




















