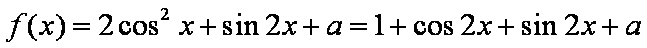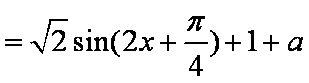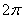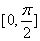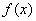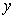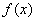- 正弦函数的对称性
- 共63题
将函数





正确答案
解析
略
知识点
已知在



(1)求角A、B、C的大小;
(2)设函数

正确答案
(1)

解析
解析:(1)由题设及正弦定理知:
∴


当




当


∴

(2) 由(1)及题设知:
当

即

它的相邻两对称轴间的距离为 
知识点
若函数


正确答案
解析
易知x=a为对称轴,所以
另解:∵x=a为对称轴,



知识点
设函数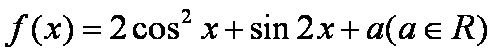
(1)求函数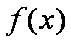
(2)当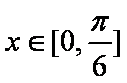
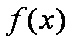
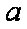
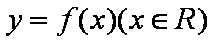
正确答案
见解析
解析
解:(1)
则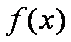
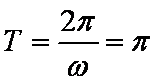
且当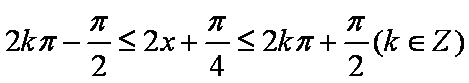
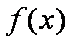
即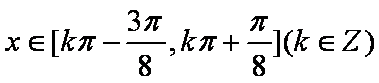
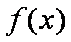
(2)当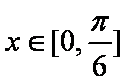
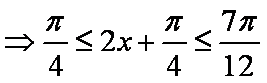
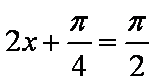
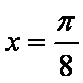
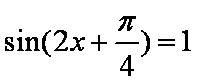
所以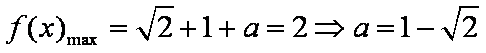
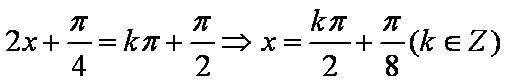
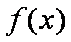
知识点
已知函数


正确答案
解析
由函数



知识点
7.将函数y=sin2x的图像上所有的点向右平行移动

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知函数①

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知函数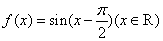
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设
(1)求f(x)的最小正周期;
(2)若函数y=f(x)与y=g(x)的图象关于直线x=1对称,求当
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知函数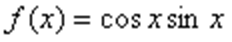
①若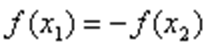
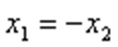
②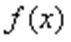
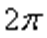
③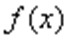
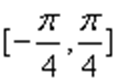
④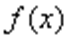
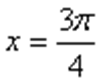
其中正确说法的序号是__________.
正确答案
③④
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析