正弦函数的对称性
共63题

· 正弦函数的对称性

正弦函数的对称性
共63题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

3．已知f（x）=sin（x+），g（x）=cos（x-），则下列结论中正确的是（）

A函数y=f（x）·g（x）的最大值为1

B函数y=f（x）·g（x）的对称中心是（,0），∈Z

C当x∈[-,]时，函数y=f（x）·g（x）单调递增

D将f（x）的图象向右平移单位后得g（x）的图象

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用正弦函数的单调性正弦函数的对称性三角函数中的恒等变换应用三角函数的最值

题型：单选题

单选题 · 5 分

8．已知函数和的图像的对称轴完全相同，若，则的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域正弦函数的对称性余弦函数的对称性

题型：单选题

单选题 · 5 分

6．已知函数f（x）=cosxsinx（x∈R），给出下列四个命题（　　）

①若f（x1）=﹣f（x2），则x1=﹣x2；

②f（x）的最小正周期是2π；

③f（x）在区间[﹣，]上是增函数；

④f（x）的图象关于直线x=对称．

A①②④

B①③

C②③

D③④

正确答案

解析

解：∵f（x）=cosxsinx=sin2x

若f（x1）=﹣f（x2），则sin2x1=﹣sin2x2=sin（﹣2x2）

∴2x1=﹣2x2+2kπ时满足条件，即x1+x2=kπ可以，故①不正确；

T=，故②不正确；

令，得﹣

当k=0时，x∈[﹣，]f（x）是增函数，故③正确；

将x=代入函数f（x）得，f（）=﹣为最小值

故f（x）的图象关于直线x=对称，④正确．

故选D．

知识点

命题的真假判断与应用三角函数的周期性及其求法正弦函数的单调性正弦函数的对称性二倍角的正弦

题型：简答题

简答题 · 14 分

15．已知a＝（sinx，－cosx），b＝（cosx，cosx），函数f（x）＝a·b＋。

（1）求f（x）的最小正周期，并求其图像对称中心的坐标；

（2）当0≤x≤时，求函数f（x）的值域。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法正弦函数的定义域和值域正弦函数的对称性三角函数中的恒等变换应用平面向量数量积的运算

题型：简答题

简答题 · 14 分

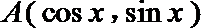
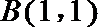
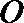
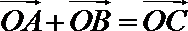
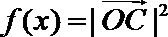
16．在直角坐标系中，已知，，为坐标原点，，。

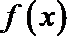
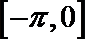
（Ⅰ）求的对称中心的坐标及其在区间上的单调递减区间；

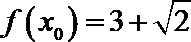
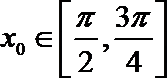
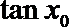
（Ⅱ）若，，求的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域正弦函数的单调性正弦函数的对称性三角函数中的恒等变换应用平面向量数量积的运算

题型：单选题

单选题 · 5 分

1.已知函数f(x)=sin(2ωx+)(ω>0)的相邻两条对称轴之间的距离为,将函数f(x)的图象向右平移个单位后,再将所有点的横坐标伸长为原来的2倍,得到g(x)的图象,若g(x)+k=0在x∈[0,]有且只有一个实数根,则k的取值范围是(　　).

A(-∞,]

B[-1,-)

C(-,]

D(-,]∪{-1}

正确答案

解析

因为f(x)相邻两条对称轴之间的距离为,结合三角函数的图象可知=.

又T==,所以ω=2,f(x)=sin(4x+).

将f(x)的图象向右平移个单位得到

f(x)=sin[4(x-)+]=sin(4x-)的图象,再将所有点的横坐标伸长为原来的2倍,得到g(x)=sin(2x-)的图象.

令2x-=t,因为x∈[0,],所以t∈[-,].

若g(x)+k=0在x∈[0,]有且只有一个实数根,

即y=sin t与y=-k在[-,]有且只有一个交点.

如图所示,由正弦函数的图象可知-≤-k<或-k=1,即-<k≤或k=-1

知识点

函数零点的判断和求解正弦函数的对称性函数y=Asin（ωx+φ）的图象变换

题型：简答题

简答题 · 12 分

20.把函数的图像向右平移 a()个单位，得到的函数的图像关于直线对称.

（1）求a的最小值；

（2）当a取最小值，求函数在区间上的值域

正确答案

（1）

∴，它关于直线对称，

∴ ∴ ∵

（2）由（1）知

即的值域为

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域正弦函数的对称性函数y=Asin（ωx+φ）的图象变换三角函数中的恒等变换应用

题型：单选题

单选题 · 5 分

5．已知函数的图象上各点的横坐标伸长到原来的3倍，再向右平移个单位，得到的函数的一个对称中心是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的对称性函数y=Asin（ωx+φ）的图象变换

题型：单选题

单选题 · 5 分

18．设函数的定义域为，若对于任意、，当时，恒有，则称点为函数图像的对称中心．研究函数的某一个对称中心，并利用对称中心的上述定义，可得到的值为（）

正确答案

解析

在中，

若，

则

，

∴的一个对称中心为，

∴

故选C．

考查方向

本题考查函数的性质，考查即时学习能力，是中档题．新定义的学习型问题，在近几年各省市高考中出现的频率很高，常以压轴题的形式出现，整合函数、数列、解析几何、三角、向量等知识，体现数学多种思想方法．

解题思路

先求的一个对称中心为，再利用对称中心的定义，求出的值．

易错点

对新定义对称中心的不理解．

知识点

正弦函数的奇偶性正弦函数的对称性

题型：单选题

单选题 · 5 分

6．若函数的图像过点，则该函数图像的一条对称轴方程是（）

正确答案

解析

将代入函数得，

得到，

又因为，

所以，再

求对称轴，，

解得，得到D答案

考查方向

本题主要考察三角函数的图像与性质，常结合图像的平移变换，求单调区间等一起出题，属中档题，是高考考察的热点之一

解题思路

将代入函数，求出值，进而根据正弦函数的对称轴列方程求出

易错点

1、正弦值为的点一个周期内有两个，分别为

2、忽略题中给出的、忽略题中给出的的取值范围

知识点

正弦函数的对称性

继续学习学习下一知识点

下一知识点 : 余弦函数的图象

百度题库 > 高考 > 理科数学 > 正弦函数的对称性

扫码查看完整答案与解析