- 正弦函数的对称性
- 共63题
1
题型：
单选题
|
3．已知f（x）=sin（x+
A函数y=f（x）·g（x）的最大值为1
B函数y=f（x）·g（x）的对称中心是（
C当x∈[-
D将f（x）的图象向右平移
正确答案
D
解析
解析已在路上飞奔，马上就到！
知识点
命题的真假判断与应用正弦函数的单调性正弦函数的对称性三角函数中的恒等变换应用三角函数的最值
1
题型：
单选题
|
8．已知函数
A
B
C
D
正确答案
C
解析
解析已在路上飞奔，马上就到！
知识点
正弦函数的定义域和值域正弦函数的对称性余弦函数的对称性
1
题型：
单选题
|
6．已知函数f（x）=cosxsinx（x∈R），给出下列四个命题（ ）
①若f（x1）=﹣f（x2），则x1=﹣x2；
②f（x）的最小正周期是2π；
③f（x）在区间[﹣
④f（x）的图象关于直线x=
正确答案
D
解析
解：∵f（x）=cosxsinx=
若f（x1）=﹣f（x2），则sin2x1=﹣sin2x2=sin（﹣2x2）
∴2x1=﹣2x2+2kπ时满足条件，即x1+x2=kπ可以，故①不正确；
T=
令
当k=0时，x∈[﹣
将x=
故f（x）的图象关于直线x=
故选D．
知识点
命题的真假判断与应用三角函数的周期性及其求法正弦函数的单调性正弦函数的对称性二倍角的正弦
1
题型：简答题
|
15．已知a＝（sinx，－cosx），b＝（cosx，
（1）求f（x）的最小正周期，并求其图像对称中心的坐标；
（2）当0≤x≤
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
三角函数的周期性及其求法正弦函数的定义域和值域正弦函数的对称性三角函数中的恒等变换应用平面向量数量积的运算
1
题型：简答题
|
16．在直角坐标系中，已知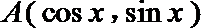
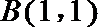
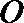
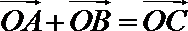
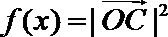
（Ⅰ）求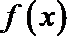
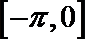
（Ⅱ）若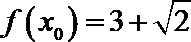
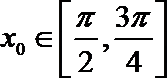
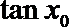
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
正弦函数的定义域和值域正弦函数的单调性正弦函数的对称性三角函数中的恒等变换应用平面向量数量积的运算
下一知识点 : 余弦函数的图象
扫码查看完整答案与解析