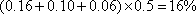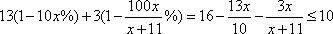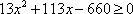- n次独立重复试验中恰好发生k次的概率
- 共66题
某班联欢晚会玩飞镖投掷游戏,规则如下:
每人连续投掷5支飞镖,累积3支飞镖掷中目标即可获奖;否则不获奖.同时要求在以下两种情况下中止投掷:①累积3支飞镖掷中目标;②累积3支飞镖没有掷中目标。
已知小明同学每支飞镖掷中目标的概率是常数

(1) 求
(2) 记小明结束游戏时,投掷的飞镖支数为

正确答案
见解析。
解析
知识点
某校一天要上语文、数学、外语、历史、政治、体育六节课,在所有可能的安排中,数学不排在最后一节,体育不排在第一节的概率是 。
正确答案
解析
略
知识点
三位同学参加跳高、跳远、铅球项目的比赛,若每人都选择其中两个项目,则有且仅有两人选择的项目完全相同的概率是().
正确答案
解析
略
知识点


正确答案
80
解析
略
知识点
李先生家住H小区,他工作在C科技园区,从家开车到公司上班路上有






(1)若走
(2)若走
(3)按照“平均遇到红灯次数最少”的要求,请你帮助李先生从上述两条路线中选择一条最好的上班路线,并说明理由.
正确答案
见解析
解析
知识点
电视传媒为了解某市100万观众对足球节目的收视情况,随机抽取了100名观众进行调查。如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图,将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”, 并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”。
(1)试估算该市“足球迷”的人数,并指出其中“铁杆足球迷”约为多少人;
(2)该市要举办一场足球比赛,已知该市的足球场可容纳10万名观众,根据调查,如果票价定为100元/张,则非“足球迷”均不会到现场观看,而“足球迷”均愿意前往现场观看。如果票价提高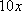
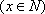
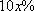
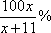
正确答案
(1)3万(2)140
解析
(1)样本中“足球迷”出现的频率=
“足球迷”的人数=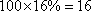
“铁杆足球迷”=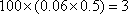
所以16万“足球迷”中,“铁杆足球迷”约有3万人.
(2)设票价为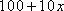
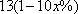
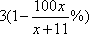
令
化简得:
解得: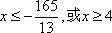
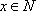
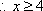
即平均票价至少定为100+40=140元,才能使前往现场观看足球比赛的“足球迷”不超过10万人.
知识点
经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高,现从一批数量很大的罗非鱼中随机地抽出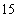
《中华人民共和国环境保护法》规定食品的汞含量不得超过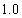
(1)检查人员从这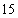
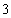
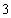
(2)若从这批数量很大的鱼中任选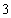
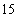
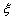

正确答案
见解析
解析
(1)记“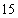
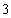
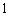
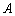
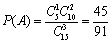
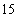
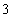
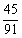
(2)依题意可知,这批罗非鱼中汞含量超标的鱼的概率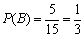
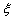
则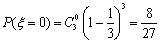
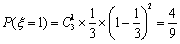
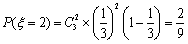
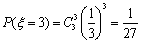
其分布列如下:
…………………………12分
所以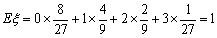
知识点
有10件不同的电子产品,其中有2件产品运行不稳定.技术人员对它们进行一一测试,直到2件不稳定的产品全部找出后测试结束,则恰好3次就结束测试的方法种数是( )
正确答案
解析
略
知识点
某班有甲、乙两个学习小组,两组的人数如下:
现采用分层抽样的方法(层内采用简单随机抽样)从甲、乙两组中共抽取
(1)求从甲组抽取的同学中恰有
(2)记


正确答案
见解析
解析
(1)解:依题意,甲、乙两组的学生人数之比为 
所以,从甲组抽取的学生人数为

设“从甲组抽取的同学中恰有

则 
故从甲组抽取的同学中恰有

(2)解:随机变量





所以,随机变量
………………11分

知识点
盒子中装有四张大小形状均相同的卡片,卡片上分别标有数字
(1)在一次试验中,求卡片上的数字为正数的概率;
(2)在四次试验中,求至少有两次卡片上的数字都为正数的概率;
(3)在两次试验中,记卡片上的数字分别为


正确答案
见解析
解析
(1)设事件A:在一次试验中,卡片上的数字为正数,则

答:在一次试验中,卡片上的数字为正数的概率是
(2)设事件B:在四次试验中,至少有两次卡片上的数字都为正数。
由(1)可知在一次试验中,卡片上的数字为正数的概率是
所以
答:在四次试验中,至少有两次卡片上的数字都为正数的概率为
(3)由题意可知,









所以随机变量
所以
知识点
扫码查看完整答案与解析