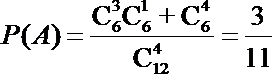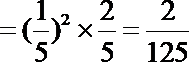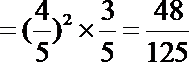- n次独立重复试验中恰好发生k次的概率
- 共66题
19.英语老师要求学生从星期一到星期四每天学习3个英语单词;每周五对一周内所学单词随机抽取若干个进行检测(一周所学的单词每个被抽到的可能性相同)
(1)英语老师随机抽了4个单词进行检测,求至少有3个是后两天学习过的单词的概率;
(2)某学生对后两天所学过的单词每个能默写对的概率为

正确答案
(1)设英语老师抽到的4个单词中,至少含有3个后两天学过的事件为A,则由题意可得
(2)由题意可得ξ可取0,1,2,3,则有P(ξ=0)
P(ξ=1)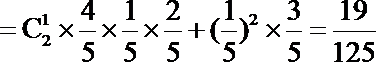
P(ξ=2) 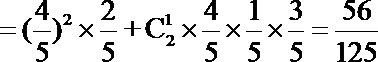
P(ξ=3)
所以ξ的分布列为:
故Eξ=0×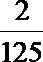
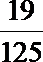
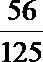
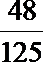
解析
解析已在路上飞奔,马上就到!
知识点
15.某地区为某类人员免费提供财会和计算机培训,参加培训者可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有





正确答案
2.7
解析
解析已在路上飞奔,马上就到!
知识点
21.已知某校5个学生的数学和物理成绩如下表
(1)假设在对这


(2)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系的,在上述表格是正确的前提下,用



(3)利用残差分析回归方程的拟合效果,若残差和在
参考数据和公式:



残差和公式为:
正确答案
(1)记事件
(2)


回归直线方程为
(3)
所以为”优拟方程”
解析
解析已在路上飞奔,马上就到!
知识点
17.前不久,省社科院发布了2013年度“城市居民幸福排行榜”,某市成为本年度城市最“幸福城市”.随后,树德中学校学生会组织部分同学,用“10分制”随机调查“新华西路”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)指出这组数据的众数和中位数;
(2)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 某同学参加3门课程的考试.假设该同学第一门课程取得优秀成绩的概率为


(1)求该生至少有1门课程取得优秀成绩的概率;
(2)求

(3)求数学期望
正确答案
事件





(1)由于事件“该生至少有1门课程取得优秀成绩”与事件“


答: 该生至少有1门课程取得优秀成绩的概率是
(2)由题意知
整理得 
由



解析
解析已在路上飞奔,马上就到!
知识点
19.甲、乙两位篮球运动员进行定点投蓝,每人各投4个球,甲投篮命中的概率为

(1)求甲至多命中2个且乙至少命中2个的概率;
(2) 求甲比乙投中的球恰好多两个的概率。
正确答案
(1)设“甲至多命中2个球”为事件A,
“乙至少命中两个球”为事件B,
由题意得,
∴甲至多命中2个球且乙至少命中2个球的概率为
(2)设甲比乙投中的球恰好多两个为事件C
则
P(C)=
解析
解析已在路上飞奔,马上就到!
知识点
18.一个口袋中装有2个白球和


(1)试用含
(2)若
(3)记三次摸球恰有一次中奖的概率为


正确答案
解:(1)∵一次摸球从

任何一个球被选出都是等可能的,其中两球颜色相同有
∴一次摸球中奖的概率
(2)若

三次摸球是独立重复试验,三次摸球恰有一次中奖的概率是

(3)设一次摸球中奖的概率为
则三次摸球恰有一次中奖的概率为

∵
∴


∴当

∵


故当
解析
解析已在路上飞奔,马上就到!
知识点
19.乒乓球台面被球网分隔成甲、乙两部分,如图,甲上有两个不相交的区域A,B,乙被划分为两个不相交的区域C,D.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在C上记3分,在D上记1分,其他情况记0分.对落点在A上的来球,队员小明回球的落点在C上的概率为,在D上的概率为;对落点在B上的来球,小明回球的落点在C上的概率为,在D上的概率为.假设共有两次来球且落在A,B上各一次,小明的两次回球互不影响.求:
(1)小明两次回球的落点中恰有一次的落点在乙上的概率;
(2)两次回球结束后,小明得分之和ξ的分布列与数学期望.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.某射击运动员在练习射击中,每次射击命中目标的概率是
正确答案
解析
根据独立重复试验的概率公式知,5次射击中,至少有4次命中的概率是




知识点
8.有6名选手参加演讲比赛,观众甲猜测:4号或5号选手得第一名;观众乙猜测:3号选手不可能得第一名;观众丙猜测:1,2,6号选手中的一位获得第一名;观众丁猜测:4,5,6号选手都不可能获得第一名.比赛后发现没有并列名次,且甲、乙、丙、丁中只有1人猜对比赛结果,此人是( )
正确答案
解析
若甲猜对,则4号或5号选手得第一名,那么乙也猜对了,不符合题意,所以甲没猜对,得第一名的是1,2,3或6号,若乙猜对,则1,2或6号得了第一名,那么丙也猜对了,所以乙没有猜对,3号没有得第一,所以得第一的是3号,所以丙也没猜对,丁猜对了,故选D。
考查方向
解题思路
逐个人去分析他所猜结果的正确性。
易错点
1.不知道从什么地方入手解决;
2.从某个观众猜起,由于信息比较多,导致混乱。
知识点
扫码查看完整答案与解析