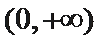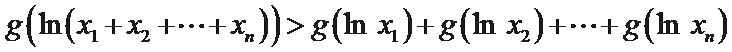- 不等式的性质
- 共451题
选做题(请考生在第11,12 ,13三题中任选两题作答,如果全做,则按前两题记分)
11.如图,AB是半圆O的直径,点C在半圆上,CD⊥AB,垂足为D,且AD=5DB,设∠COD=

12.已知在平面直角坐标系xOy中,圆C的参数方程为


13.不等式
正确答案
11.
12.
13.[1,3]
解析
解析已在路上飞奔,马上就到!
知识点
7.变量x,y满足约束条件

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 若直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知实数


正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
21.对于函数f(x)(x∈D),若x∈D时,恒有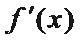
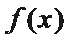
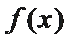
(Ⅰ)当函数f(x)=m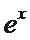
(Ⅱ)若函数g(x)为(0,+∞)上的J函数,试比较g(a)与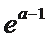
正确答案
解:(Ⅰ)由
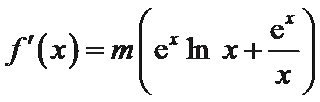
因为函数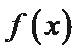
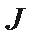
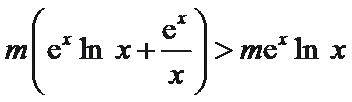
即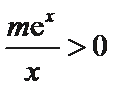
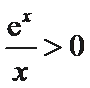
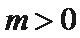
即
(Ⅱ)①构造函数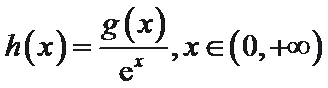
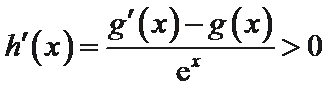
可得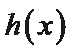
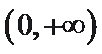
当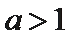
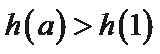
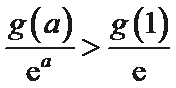
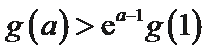
当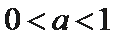
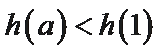
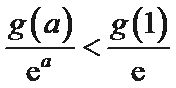
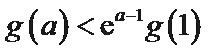
当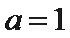
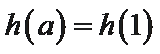
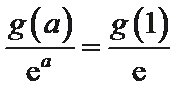
②因为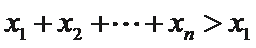
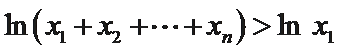
由①可知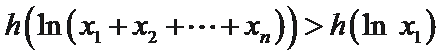

整理得
同理可得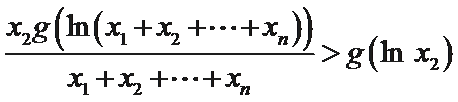
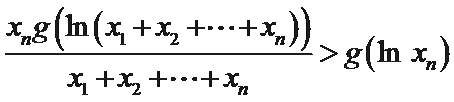
把上面
可得
解析
解析已在路上飞奔,马上就到!
知识点
10. 设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请在22~24题中任选一题作答
22.选修4-1:几何证明选讲
如图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(I)求AC的长;
(II)求证:BE=EF.
23.选修4-4:坐标系与参数方程
在极坐标系中, O为极点, 半径为2的圆C的圆心的极坐标为
(I)求圆C的极坐标方程;
(II)



24.选修4-5:不等式选讲
已知

(I)求证:

(II)若

正确答案
22.
23.
24.
解析
解析已在路上飞奔,马上就到!
知识点
13. 变量




正确答案
-2
解析
解析已在路上飞奔,马上就到!
知识点
14.已知点A是不等式组


正确答案
[-1,1]
解析
解析已在路上飞奔,马上就到!
知识点
8.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析