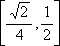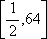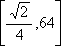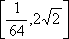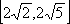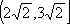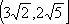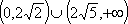不等式的性质
共451题

· 不等式的性质

不等式的性质
共451题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

设不等式组表示的平面区域为，在区域内随机取一个点，则此点到直线的距离大于2的概率是

正确答案

解析

略

知识点

不等式的性质

题型：单选题

单选题 · 5 分

已知是不等式组所表示的平面区域内的两个不同的点，则的最大值是（）

正确答案

解析

略

知识点

不等式的性质

题型：单选题

单选题 · 5 分

设变量满足约束条件则的取值范围是( )

正确答案

解析

略

知识点

不等式的性质

题型：填空题

填空题 · 5 分

已知且,则。

正确答案

解析

略

知识点

不等式的性质

题型：简答题

简答题 · 14 分

已知数列中,,且

（1）求证：;

（2）设,是数列的前项和,求的解析式;

（3）求证：不等式对恒成立.

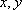
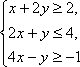
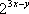
正确答案

见解析。

解析

知识点

不等式的性质

题型：填空题

填空题 · 5 分

观察以下几个等式：⑴ ； ⑵ ；

(3) ，归纳其特点可以获得一个猜想是：。

正确答案

或

解析

略

知识点

不等式的性质

题型：单选题

单选题 · 5 分

甲、乙、丙三名运动员在某次测试中各射击20次，三人测试成绩的频率分布条形图分别如图1，图2和图3，若分别表示他们测试成绩的标准差，则它们的大小关系是…………………………………………………………………… （）

正确答案

解析

略

知识点

不等式的性质

题型：简答题

简答题 · 13 分

将一个正整数表示为的形式，其中，，且，记所有这样的表示法的种数为（如4=4，4=1+3，4=2+2，4=1+1+2，4=1+1+1+1，故）.

（1）写出的值，并说明理由；

（2）对任意正整数，比较与的大小，并给出证明；

（3）当正整数时，求证：。

正确答案

见解析

解析

（1）解：因为3=3，3=1+2，3=1+1+1，所以。

因为5=5，5=2+3，5=1+4，5=1+1+3，5=1+2+2，5=1+1+1+2，5=1+1+1+1+1，

所以。 ……………………………………3分

（2）结论是.

证明如下：由结论知，只需证

因为，把的一个表示法中的去掉，就可得到一个的表示法；反之，在的一个表示法前面添加一个“1+”，就得到一个的表示法，即的表示法中的表示法种数等于的表示法种数，

所以表示的是的表示法中的表示法数，是的表示法中的表示法数。

同样，把一个的的表示法中的加上1，就可得到一个的的表示法，这样就构造了从的的表示法到的的表示法的一个对应.

所以有……………………………………9分

（3）由第（2）问可知：

当正整数时，.

又所以.

对于*式，分别取为，将所得等式相加得.

即。 ……………………………………13分

知识点

不等式的性质不等式的证明

题型：填空题

填空题 · 5 分

已知在直线运动，当函数取得最大值时，点的坐标为

正确答案

解析

略

知识点

不等式的性质

题型：单选题

单选题 · 5 分

设不等式组表示的平面区域为.若圆不经过区域上的点,则的取值范围是（）

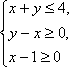
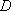
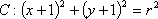
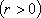
正确答案

解析

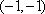
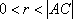
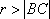
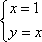
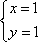
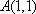
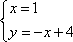
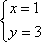
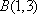
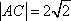
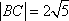
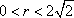
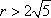
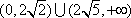
不等式对应的区域为ABE.圆心为，区域中，A到圆心的距离最小，B到圆心的距离最大，所以要使圆不经过区域D,则有或.由得，即。由，得，即。所以，，所以或，即的取值范围是。

知识点

不等式的性质

继续学习学习下一知识点

下一知识点 : 不等式的应用

百度题库 > 高考 > 理科数学 > 不等式的性质

扫码查看完整答案与解析