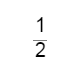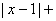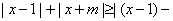- 不等式的性质
- 共451题
已知实数x,y满足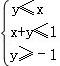
正确答案
解析
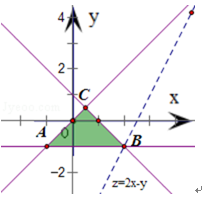
作出不等式组表示的平面区域,得到如图的△ABC及其内部,
其中A(﹣1,﹣1),B(2,﹣1),C(0.5,0.5)
设z=F(x,y)=2x﹣y,将直线l:z=2x﹣y进行平移,
当l经过点B时,目标函数z达到最大值
∴z最大值=F(2,﹣1)=5
故选:C
知识点
若关于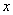
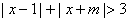
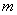
正确答案
解析
由题意知,不等式


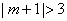
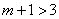
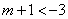
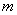
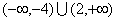
知识点
已知变量




正确答案
9
解析
先根据约束条件画出变量








知识点
不等式
正确答案


解析
略
知识点
已知函数









(1)求
(2)已知实数t∈R,求函数
(3)令


存在实数




正确答案
见解析。
解析






由题意可得

∴
(2)
令


∴



①当

②当

③当


所以

∴
①当


得

∴ 由

从而有
②当


由

∴
③当

得
∴综合①、②、③得
知识点
已知数列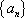

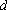
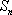

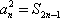

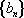
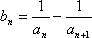
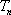
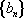
(1)求
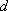
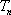
(2)若对任意的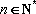
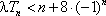
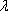
正确答案
见解析
解析
(1)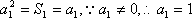
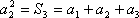
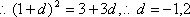
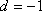
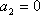
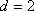
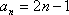

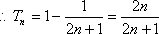
……………………………. 6分
(2)当
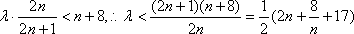
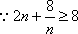
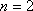
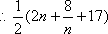
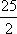
因此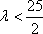
当
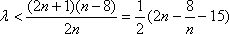
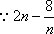
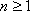
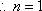

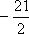
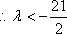

综上,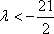
知识点
在直角坐标系中,若不等式组

正确答案
解析
由题意可知,直线






知识点
对任意的实数


正确答案
解析
当









知识点
若等式






正确答案
-5
解析
略
知识点
在



(1)若



(2)若



正确答案
见解析。
解析
(1)


(2)
得
知识点
扫码查看完整答案与解析