- 不等式的性质
- 共451题
已知关于



正确答案
见解析。
解析
若

若


即

所以


解得
知识点
已知:函数

(1)求


(2)若不等式


(3)如果关于


正确答案
见解析
解析
(1)



或 


∴



(2)不等式

∴
设
∴

∴
(3)

令


记方程



记


∴
知识点
(1) 已知
(2) 已知







(3) 已知

正确答案
见解析
解析
(1)设





(2)设M(

则有:
所以:

故


(3)
当


当
……………………………….14分
知识点
已知x,y,z∈R,且x﹣2y﹣3z=4,求x2+y2+z2的最小值。
正确答案
见解析
解析
由柯西不等式,得[x+(-2)y+(-3)z]2≤[12+(-2)2+(-3)2](x2+y2+z2),
即(x-2y-3z)2≤14(x2+y2+z2)
即16≤14(x2+y2+z2)。
所以
知识点
已知x,y,z均为正数,求证:
正确答案
见解析。
解析
因为x,y,z都是为正数,所以
同理可得
将上述三个不等式两边分别相加,并除以2,得
知识点
为了保养汽车,维护汽车性能,汽车保养一般都在购车的4S店进行,某地大众汽车4S店售后服务部设有一个服务窗口专门接待保养预约。假设车主预约保养登记所需的时间互相独立,且都是整数分钟,对以往车主预约登记所需的时间统计结果如下:
从第—个车主开始预约登记时计时(用频率估计概率),
(1)估计第三个车主恰好等待4分钟开始登记的概率:
(2)X表示至第2分钟末已登记完的车主人数,求X的分布列及数学期望。
正确答案
见解析
解析
解析:设Y表示车主登记所需的时间,用频率估计概率,Y的分布如下:
(1)A表示事件“第三个车主恰好等待4分钟开始登记”,则事件A对应三种情形:
①第一个车主登记所需时间为1分钟,且第二个车主登记所需的时间为3分钟;
②第一个车主登记所需的时间为3分钟,且第二个车主登记所需的时间为1分钟;
③第一个和第二个车主登记所需的时间均为2分钟。
所以

(2)X所有可能的取值为:0,1,2.X=0对应第一个车主登记所需的时间超过2分钟,所
以
第二个车主登记所需时间超过1分钟,或第一个车主登记所需的时间为2分钟,
所以
车主登记所需的时间均为1分钟,所以

所以X的分布列为


知识点
解不等式x|x﹣4|﹣3<0。
正确答案
见解析
解析
原不等式转化为:
解得
即
知识点
某种家用电器每台的销售利润与该电器的无故障使用时间















(1)求


(2)记

正确答案
见解析
解析
解析:(1)由已知得

∵


∴

(2)






故
知识点
解不等式
正确答案
见解析
解析
当


当


当


综上所述,原不等式的解集为
知识点
在△ABC中,E、F分别为AB,AC中点.P为EF上任一点,实数x,y满足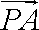
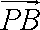
y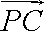
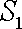
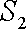
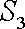
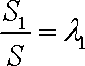
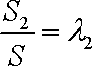
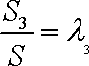
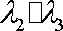
正确答案
解析
由题意知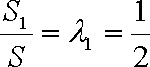
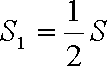
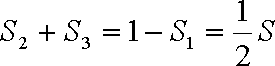
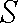
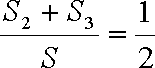
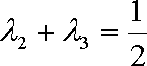
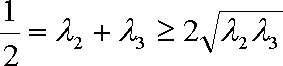
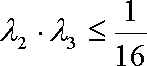
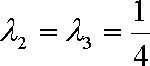
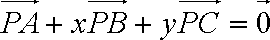
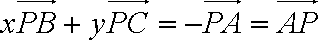
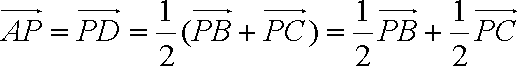
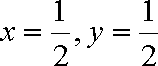
知识点
扫码查看完整答案与解析