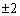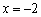平面向量的概念及线性运算、平面向量基本定理
共611题

平面向量的概念及线性运算、平面向量基本定理
共611题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

已知矩形ABCD中，，，E、F分别是BC、CD的中点，则等于。

正确答案

解析

略

知识点

平面向量的概念辨析

题型：填空题

填空题 · 5 分

在平面直角坐标系中，将点绕原点逆时针旋转到点，那么点的坐标为____，若直线的倾斜角为，则的值为。

正确答案

；

解析

略

知识点

平面向量的概念辨析

题型：填空题

填空题 · 5 分

在边长为1的正方形ABCD中，E、F分别为BC、DC的中点，则向量。

正确答案

解析

略

知识点

平面向量的概念辨析

题型：填空题

填空题 · 5 分

已知两个不相等的非零向量两组向量和均由2个和3个排列而成.记，表示所有可能取值中的最小值.则下列命题的是_________（写出所有正确命题的编号）.

①有5个不同的值. ②若则与无关. ③若则与无关.

④若，则. ⑤若则与的夹角为

正确答案

②④

解析

此题以向量知识为背景，考察排列、重组、配对、构造、分类讨论、等价转化等数学素养和创新意识。

知识点

平面向量的概念辨析

题型：简答题

简答题 · 14 分

设抛物线的焦点为，点，线段的中点在抛物线上. 设动直线与抛物线相切于点，且与抛物线的准线相交于点，以为直径的圆记为圆。

（1）求的值；

（2）试判断圆与轴的位置关系；

（3）在坐标平面上是否存在定点，使得圆恒过点？若存在，求出的坐标；若不存在，说明理由。

正确答案

见解析。

解析

（1）利用抛物线的定义得，故线段的中点的坐标为，代入方程得，解得。

（2）由（1）得抛物线的方程为，从而抛物线的准线方程为

由得方程，

由直线与抛物线相切，得

且，从而，即，

由，解得，

∴的中点的坐标为

圆心到轴距离，

∵

∵，

∴ 当时，，圆与轴相切；

当时，，圆与轴相交；

(或，以线段为直径圆的方程为:

令得　

∴ 当时，，圆与轴相切；

当时，，圆与轴相交；

（3）方法一：假设平面内存在定点满足条件，由抛物线对称性知点在轴上，设点坐标为，

由（2）知，

∴ 。

由得，

所以，即或

所以平面上存在定点，使得圆恒过点.

证法二：由（2）知，，的中点的坐标为

所以圆的方程为

整理得

上式对任意均成立，

当且仅当，解得

知识点

平面向量的概念辨析

题型：单选题

单选题 · 5 分

若向量满足，则的值为（）

C-1

正确答案

解析

略

知识点

平面向量的概念辨析

题型：填空题

填空题 · 5 分

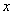
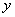
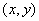
在平面直角坐标系中，如果与都是整数，就称点为整点，下列命题中正确的是_____________（写出所有正确命题的编号）。

①存在这样的直线，既不与坐标轴平行又不经过任何整点

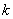
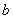
②如果与都是无理数，则直线不经过任何整点

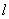
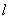
③直线经过无穷多个整点，当且仅当经过两个不同的整点

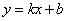
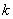
④直线经过无穷多个整点的充分必要条件是：与都是有理数

⑤存在恰经过一个整点的直线

正确答案

①③⑤

解析

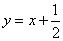
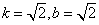
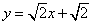
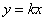
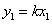
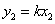
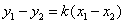
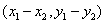
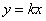
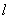
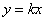
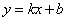
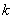
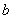
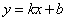
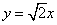
令满足①，故①正确；若，过整点（－1,0），所以②错误；设是过原点的直线，若此直线过两个整点，则有，，两式相减得，则点也在直线上，通过这种方法可以得到直线经过无穷多个整点，通过上下平移得对于也成立，所以③正确；与都是有理数,直线不一定经过整点，④错误；直线恰过一个整点，⑤正确。

知识点

平面向量的概念辨析

题型：单选题

单选题 · 5 分

对于直线m，n和平面α，β，使m⊥α成立的一个充分条件是（　　）

Am⊥n，n∥α

Bm∥β，β⊥α

Cm⊥β，n⊥β，n⊥α

Dm⊥n，n⊥β，β⊥α

正确答案

解析

对于A，”m⊥n，n∥α”，如正方体中AB⊥BC，BC∥平面A′B′C′D′，但AB与平面A′B′C′D′不垂直，故推不出m⊥α，故A不正确；

对于B，“m∥β，β⊥α”，如正方体中A′C′∥面ABCD，面ABCD⊥面BCC′B′，但A′C′与平面BCC′B′不垂直，推不出m⊥α，故不正确；

对于C，根据m⊥β，n⊥β，得m∥n，又n⊥α，

根据线面垂直的判定，可得m⊥α，可知该命题正确；

对于D，“m⊥n，n⊥β，β⊥α”，如正方体中AD′⊥AB，AB⊥面BCC′B′，面ABCD⊥面BCC′B′，但AD′与面BCC′B′不垂直，故推不出m⊥α，故不正确。

知识点

平面向量的概念辨析

题型：单选题

单选题 · 5 分

设向量，，且方向相反，则的值是（）。

B-2

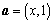
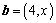
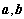
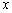
正确答案

解析

因为向量，且方向相反，所以且，故

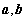
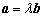
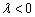
知识点

平面向量的概念辨析

题型：单选题

单选题 · 5 分

设平面向量，若//，则等于（）

正确答案

解析

略

知识点

平面向量的概念辨析

继续学习学习下一知识点

下一知识点 : 平面向量的数量积及其应用

百度题库 > 高考 > 理科数学 > 平面向量的概念及线性运算、平面向量基本定理

扫码查看完整答案与解析