平面向量的概念及线性运算、平面向量基本定理
共611题

平面向量的概念及线性运算、平面向量基本定理
共611题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 4 分

4. 点是所在平面内的一点，满足则点是的（）

A外心

B内心

C重心

D垂心

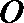
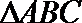
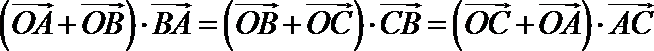
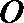
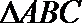
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

相等向量与相反向量

题型：单选题

单选题 · 5 分

5．关于平面向量的命题

①·=·且≠时，必有 = ；

②如//时，必存在唯一实数使=；

③，，互不共线时，必与不共线；

④与共线且与也共线时，则与必共线。

其中正确命题个数有（）

A0个

B1个

C2个

D3个

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用平行向量与共线向量相等向量与相反向量

题型：单选题

单选题 · 5 分

5．已知各项均不为零的数列，定义向量，下列命题中真命题是（）

A若成立，则数列是等差数列

B若成立，则数列是等比数列

C若成立，则数列是等差数列

D若成立，则数列是等比数列

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

相等向量与相反向量

题型：单选题

单选题 · 5 分

3．已知某随机变量X的概率密度函数为P(x)=,则随机变量X落在区间(1,2)内的概率为（）

Ae2+e

Ce2-e

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

相等向量与相反向量

题型：简答题

简答题 · 14 分

20．已知A(,)，B(,)是函数的图象上的任意两点（可以重合），点M在直线上，且．

（1）求+的值及+的值

（2）已知，当时，+++，求；

（3）在（2）的条件下，设=，为数列{}的前项和，若存在正整数、，使得不等式成立，求和的值．

正确答案

解：
　　（1）∵点M在直线x=上，设M.
　　又＝，即，，
　　∴+=1.

① 当=时，=，+=；

② 当时，，
　　+=+===
　　综合①②得，+.
　　（Ⅱ）由（Ⅰ）知，当+=1时, +
　　∴，k=.

n≥2时，+++　，　　　　　 ①
　　　，　　　　　②
　　①＋②得，2=-2(n-1),则=1-n.　　
　　当n=1时，=0满足=1-n. ∴=1-n.
　　（Ⅲ）==，=1++=.
　　.
　　=2-，=-2+=2-，
　　∴，、m为正整数，∴c=1，
　　当c=1时，，
　　∴1<<3，
　　∴m=1.

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法相等向量与相反向量由递推关系式求数列的通项公式倒序相加法求和数列与不等式的综合

题型：填空题

填空题 · 4 分

4．某学校的某一专业从8名优秀毕业生中选派5名支援中国西部开发建设，其中甲同学必须被选派的概率是______

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

相等向量与相反向量

题型：填空题

填空题 · 5 分

12. 已知 _________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

相等向量与相反向量

题型：简答题

简答题 · 12 分

16.已知向量函数

（1）求函数的解析式，并求其最小正周期;

（2）求函数图象的对称中心坐标与对称轴方程.

（3）求函数的单调递增区间；

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

相等向量与相反向量

题型：填空题

填空题 · 4 分

13．如图所示，在边长为2的正六边形中，动圆的半径为1，圆心在线段（含端点）上运动，是圆上及内部的动点，设向量为实数），则的最大值为（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

相等向量与相反向量

题型：单选题

单选题 · 5 分

2.设变量x，y满足约束条件：.则目标函数z=2x+3y的最小值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

相等向量与相反向量

继续学习学习下一知识点

下一知识点 : 平面向量的数量积及其应用

百度题库 > 高考 > 理科数学 > 平面向量的概念及线性运算、平面向量基本定理

扫码查看完整答案与解析