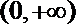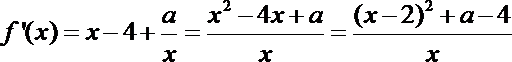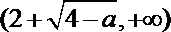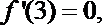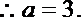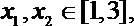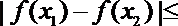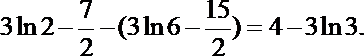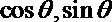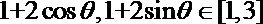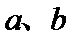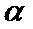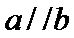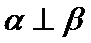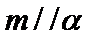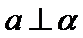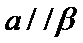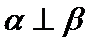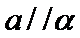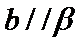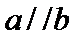- 平面向量的概念及线性运算、平面向量基本定理
- 共611题
21.设动点




(1)求点
(2)设圆








正确答案
(1)依题意知,
动点



曲线

∵ 
∴ 曲线
(2)设圆的圆心为
∵ 圆

∴ 圆的方程为
令
设圆与

方法1:不妨设

∴
又∵点


∴ 

∴当

方法2:∵
∴
又∵点

∴ 

∴当

解析
解析已在路上飞奔,马上就到!
知识点
12.已知点




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知非零向量






(1)当

(2)设数列





正确答案
(1)


(2)∵ 
∴ 
∴ 

∴ 
∴ 

∴
解析
解析已在路上飞奔,马上就到!
知识点
6.已知:0<









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知向量a=(
正确答案
解析
设选项中的向量与a的夹角为θ,对于选项A,由于cos θ=-



知识点
20.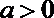
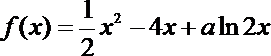
(1)求函数 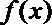
(2)当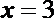
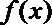
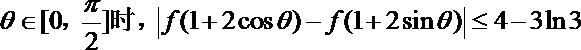
正确答案
(1)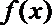
① 当
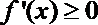
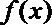
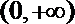
② 当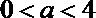
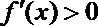
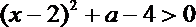
解得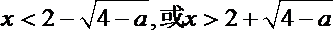
因此,函数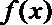
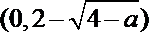
内也单调递增.
令
解得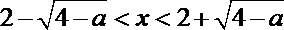
因此,函数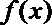
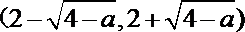
(2)当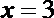
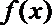

由(1)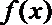
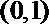
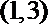
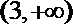
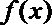
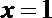
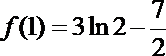
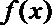
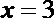

故在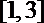
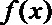
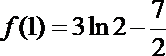

对于任意的
当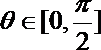
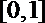
从而
解析
解析已在路上飞奔,马上就到!
知识点
4.设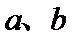
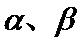
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
正确答案
D
解析
略
知识点
1.满足M
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 若



正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析