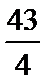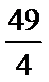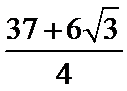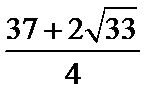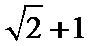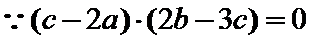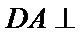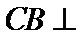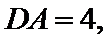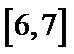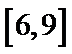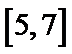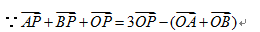平面向量的概念及线性运算、平面向量基本定理
共611题

平面向量的概念及线性运算、平面向量基本定理
共611题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 4 分

3、已知平行直线，则的距离_______________

正确答案

解析

知识点

向量的加法及其几何意义

题型：单选题

单选题 · 5 分

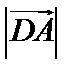
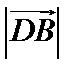
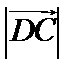
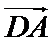
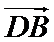
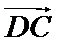
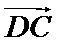
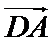
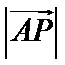
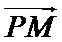
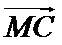
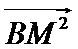
10．在平面内，定点A，B，C，D满足 ==,﹒=﹒=﹒=-2，动点P，M满足 =1，=，则的最大值是

正确答案

知识点

向量的加法及其几何意义

题型：单选题

单选题 · 5 分

4.设，是向量，则“”是“”的（）

A充分而不必要条件

B必要而不充分条件

C充分必要条件

D既不充分也不必要条件

正确答案

解析

，故是既不充分也不必要条件，故选D

考查方向

1.充分必要条件；2.平面向量数量积.

解题思路

由向量数量积的定义(为，的夹角)可知，数量积的值、模的乘积、夹角知二可求一，求解夹角与模的题目在近年高考中出现的频率很高，应熟练掌握其解法.

易错点

向量数量积的定义式(为，的夹角)的正确表示.

知识点

向量的加法及其几何意义

题型：单选题

单选题 · 5 分

7．设为所在平面内一点，则（）

正确答案

解析

由题知

=，故选A.

考查方向

本题主要考察了平面向量的基本定理，属于中档题，是高考的热点，解决此类题的关键是会利用平面向量的基本定理，用两个不共线的向量表示平面内任一向量。

解题思路

本题考查平面向量的基本定理，具体解题步骤如下：1.在三角形ABD中用向量加法的三角形法则。2.不断把向量用基底表示.

易错点

本题易在向量的表示过程中出现错误。

知识点

向量的加法及其几何意义

题型：简答题

简答题 · 10 分

请考生在三道题中任选一题作答，如果多做，则安所做的第一题计分。作答时请写清题号。

【选修4-1：几何证明选讲】请回答28、29题。

如图，AB是⊙的直径，AC是⊙的切线，BC交⊙于点E。

【选修4-4；坐标系与参数方程】请回答30、31题。

在直角坐标系中，直线:x=,圆：，以坐标原点为极点，轴的正半轴为极轴建立极坐标系。

【选修4-5：不等式选讲】请回答32、33题。

已知函数f（x）=|x+1|-2|x-a|，则a>0.

28.若D为AC的中点，证明：DE是⊙的切线；

29.若CA=CE，求∠ACB的大小。

30.求，C2的极坐标方程。

31.若直线C3的极坐标为=（ρR）,设C2与C3的交点为M，N,求△C2MN的面积

32.当a=1时，求不等式f（x）>1的解集；

33.若f（x）的图像与x轴围成的三角形面积大于6，求a的取值范围.

第(1)小题正确答案及相关解析

正确答案

第(2)小题正确答案及相关解析

正确答案

第(3)小题正确答案及相关解析

正确答案

第(4)小题正确答案及相关解析

正确答案

第(5)小题正确答案及相关解析

正确答案

第(6)小题正确答案及相关解析

正确答案

题型：填空题

填空题 · 5 分

15.已知向量a，b，c，满足|a|=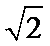，|b|=a·b=3，若(c-2a)·(2b-3c)=0，则|b-c|的最大值是____；

正确答案

解析

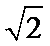
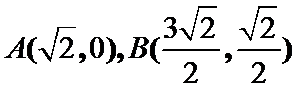
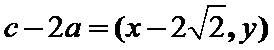
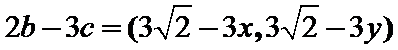
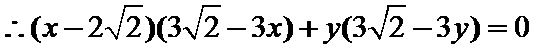
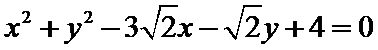
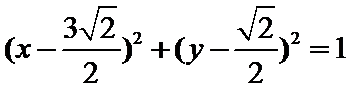
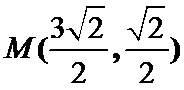
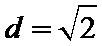
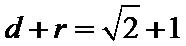
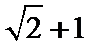
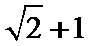
因为|a|=，|b|=a·b=3，所以可求向量a和向量b的夹角为45度。设向量OA=向量a,向量OB等于向量b,O为坐标原点，则|b-c|=|BC|.,设C(x,y),则，，整理可得，，即。所以点C的轨迹为以为圆心，以为半径的圆。所以点B到圆心M的距离，所以BC的最大距离为,所以|b-c|的最大值为，故填。

考查方向

平面向量的数量积的运算

解题思路

先根据已知条件，求出向量a,b的坐标，利用向量垂直得出c的方程，转化为平面几何中的距离问题

易错点

求最大值

知识点

向量的加法及其几何意义

题型：单选题

单选题 · 5 分

7.在平面直角坐标系中，若不等式组（为常数）表示的区域面积等于，则的值为 ( )

正确答案

解析

由题可知，A(2,2a+1),B(1,a+1), ，D(2，0)

所以，所以

考查方向

平面向量的应用简单线性规划

解题思路

建立适当的坐标系，利用线性规划理论，根据区域的面积求参数的值

知识点

向量的加法及其几何意义

题型：单选题

单选题 · 5 分

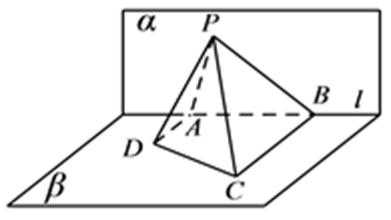
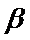
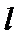
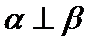
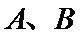
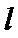
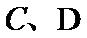
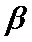
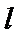
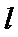
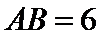
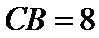
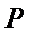
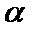
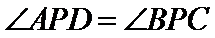
8.如图，已知平面=，.是直线上的两点，是平面内的两点，且，，，.是平面上的一动点，且有，则四棱锥体积的最大值是（）

A48

正确答案

解析

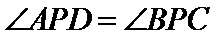
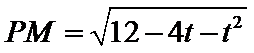
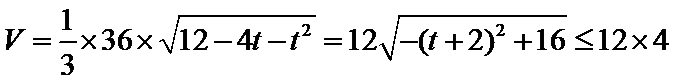
由题意知：三角形PAD，三角形PBC是直角三角形，有，所以三角形PAD相似于三角形PBC，因为DA=4，CB=8，所以PB=2OA.作PM垂直于AB于M,令AM=t.则即为四棱柱的高，所以

，所以最小值为48

考查方向

线面垂直，面面垂直，四棱锥的体积，求最大值

解题思路

先根据已知条件，用参数表示四棱锥的体积，然后找到最大值的情况。

易错点

判断最大值时的情况

知识点

向量的加法及其几何意义

题型：单选题

单选题 · 5 分

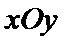
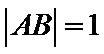
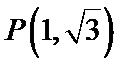
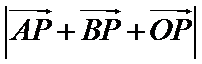
9.在平面直角坐标系中，已知点A,B分别为x轴，y轴上一点，且，若点，则的取值范围是（）

正确答案

解析

考查方向

本题主要考察了向量的几何意义，主要考察了向量的平行四边形法则，向量的坐标表示及其代数运算，考察了利用三角函数求最值问题，平面向量问题在高考中是常见题型，向量和很多知识都是联系，所以思路多，但是不好构建易出错。

解题思路

使用向量的几何意义，

易错点

本题易错于几何意义的转换，或者在使用坐标化的过程中A，B两点的形成过程，代数法构建过程繁琐，学生易计算出错，

知识点

三角函数中的恒等变换应用向量的加法及其几何意义

题型：单选题

单选题 · 5 分

已知为所在平面内的一点，且．若点在的内部(不含边界)，则实数的取值范围是____．

正确答案

考查方向

本题主要考查平面向量几何运算的性质及平行四边形法则的应用等知识,意在考查考生用数形结合思想解决问题的能力，在近几年的各省高考题出现的频率较高，较易。

易错点

1、本题在根据平行四边形法则由转换成平行四边形上易出错。

知识点

向量的加法及其几何意义

继续学习学习下一知识点

下一知识点 : 平面向量的数量积及其应用

百度题库 > 高考 > 理科数学 > 平面向量的概念及线性运算、平面向量基本定理

扫码查看完整答案与解析