• 职业资格类
  • 建筑类
  • 学历类
  • 财会类
  • 医药类
  • 全部考试
职业资格类
建筑类
学历类
财会类
计算机类
公务员
医药类
  • 平面向量的概念及线性运算、平面向量基本定理
  • 共611题
  • 平面向量的概念及线性运算、平面向量基本定理
  • 共611题

热门试卷

X 查看更多试卷
1
题型：填空题
|
填空题 · 5 分

13． 如图，在四边形中，，为的中点，且，则 ．

正确答案

1

解析

解析已在路上飞奔，马上就到！

知识点

平面向量的基本定理及其意义向量在几何中的应用
1
题型： 单选题
|
单选题 · 5 分

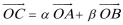
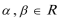
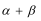
3．平面坐标系中，0为坐标原点，点A（3，1），点B（-1，3），若点C满足，其中且=1，则点C的轨迹方程为（    ）

A2x+y=l

Bx+2y=5

Cx+y=5

Dx—y=1

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

平面向量的基本定理及其意义平面向量的坐标运算直接法求轨迹方程
1
题型：填空题
|
填空题 · 5 分

3.下列各组向量中：

①e1＝（－1,2），e2＝（5,7）；

②e1＝（3,5），e2＝（6,10）；

③e1＝（2，－3），e2＝。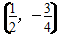

有一组能作为表示它们所在平面内所有向量的基底，这一组是（       ）（填序号）。

正确答案

①

解析

解析已在路上飞奔，马上就到！

知识点

平面向量的基本定理及其意义
1
题型： 单选题
|
单选题 · 5 分

10．已知为平面上的一个定点，A、B、C是该平面上不共线的三个动点，点满足条件，则动点的轨迹一定通过的（   ）

A重心

B垂心

C外心

D内心

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

平面向量的基本定理及其意义向量在几何中的应用
1
题型：填空题
|
填空题 · 5 分

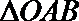
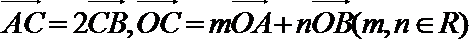
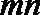
11.如图，已知C为边AB上一点，且,则=（    ）     

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面向量的基本定理及其意义向量在几何中的应用
1
题型：填空题
|
填空题 · 5 分

9.正三角形ABC内有一点M满足,∠MCA=45°,则=______.

正确答案

解析

设正三角形边长为a,∵∠MCA=45°,∴cos 45°=.

又∵=(m+n)·=ma2+a2,

∴=ma+na.同理∠MCB=15°,=cos 15°==a2+na2,解得=,所以=ma+a,化简得=.

知识点

平面向量的基本定理及其意义向量在几何中的应用
1
题型： 单选题
|
单选题 · 5 分

9．如图，设P、Q为△ABC内的两点，且，，则△ABP的面积与△ABQ的面积之比为（    ）

A

B

C

D

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

平面向量的基本定理及其意义向量在几何中的应用
1
题型： 单选题
|
单选题 · 3 分

24．将一圆的六个等分点分成两组相间的三点，它们所构成的两个正三角形扣除内部六条线段后可以形成一正六角星，如图所示的正六角星的中心为点，其中分别为点到两个顶点的向量. 若将点到正六角星12个顶点的向量，都写成为的形式，则的最大值为

A3

B4

C5

D6

正确答案

C

解析

因为想求的最大值，所以考虑下图中的6个顶点之间向量即可. 讨论如下:   

①因为所以；  

②因为所以；  

③因为所以；  

④因为

所以；  

⑤因为所以；

⑥因为所以；

因此，的最大值为。A选项不正确，B选项不正确，D选项不正确，所以选C选项。

考查方向

本题主要考查向量的加法减法运算及几何意义

解题思路

表示向量，利用向量加法运算法则讨论，即可得到结果。A选项不正确，B选项不正确，D选项不正确，所以选C选项。

易错点

本题易在表示向量时发生错误。

知识点

平面向量的基本定理及其意义
1
题型： 单选题
|
单选题 · 5 分

7． O是平面上一定点，A、B、C平面上不共线的三点，动点P满足 则P点的轨迹一定经过ABC的（ ）

A外心

B内心

C重心

D垂心

正确答案

B

解析

由

再由共线定理知点必经过ABC的内心，（重垂内外，中高角直）所以选B选项。

考查方向

本题主要考查了向量的运算和几何体现，常考的有向量的数量积和坐标运算，以及在圆锥曲线上角度、长度等的应用。

解题思路

先对原式变形可得

所以

再由共线定理知点必经过ABC的内心；

易错点

1、不理解向量的意义； 

2、对三角形的各心与对应线没有对应起来。

知识点

平面向量的基本定理及其意义向量在几何中的应用
1
题型： 单选题
|
单选题 · 5 分

10．如图所示，在正六边形ABCDEF中，点P是△CDE内(包括边界)的一个动点，

设，则的取值范围是

AA．

B

C

D

正确答案

B

解析

这类题型需要建立好坐标系，根据坐标系找可行域更可行  

考查方向

向量在几何中的应用；平面向量的基本定理及其意义

解题思路

先建立直角坐标系，然后求出EC和CD的方程，找到可行域，将平面向量用坐标形式表示，带入可行域中，求得。

易错点

建立坐标系错误、计算能力弱

知识点

平面向量的基本定理及其意义向量在几何中的应用
继续学习 学习下一知识点
下一知识点 : 平面向量的数量积及其应用
百度题库 > 高考 > 理科数学 > 平面向量的概念及线性运算、平面向量基本定理

扫码查看完整答案与解析

  • 上一题
  • 1/10
  • 下一题