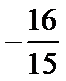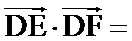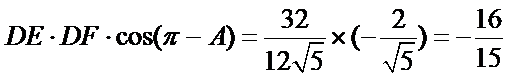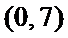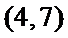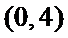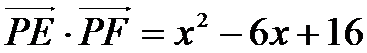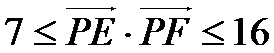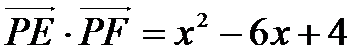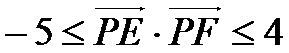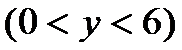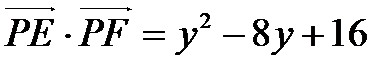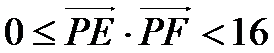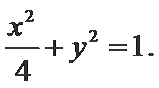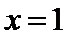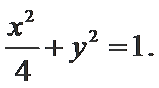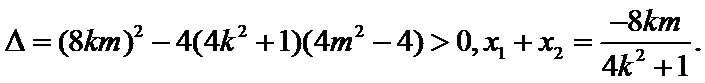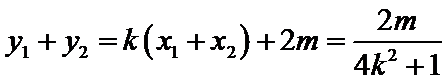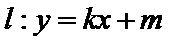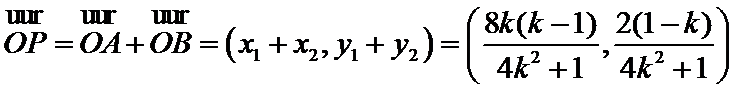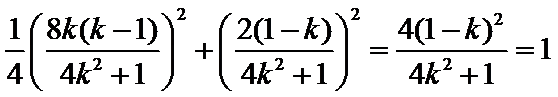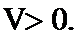- 向量在几何中的应用
- 共173题
9.如图,设P、Q为△ABC内的两点,且

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知菱形






正确答案
2
解析


考查方向
解题思路
本题考查运用平面向量在几何中的应用,解题步骤如下:建立如图所示直角坐标系,
则

易错点
本题必须注意审题,忽视则会出现错误。
知识点
7. O是平面上一定点,A、B、C平面上不共线的三点,动点P满足

正确答案
解析
由
再由共线定理知点

考查方向
解题思路
先对原式变形可得
所以
再由共线定理知点

易错点
1、不理解向量
2、对三角形的各心与对应线没有对应起来。
知识点
16.已知ΔABC满足

正确答案
[1,3]
解析
由
整理得:
由
得
将(1)代入(2)得到
三角形BCM中余弦定理可得
(3)、(4)联立整理得
三角形ACM中余弦定理可得
将(1)、(3)、(5)代入(6)得
因此
考查方向
解题思路
1、根据
2、结合图形利用正余弦定理分析求解
易错点
结合图形利用正余弦定理分析求解
知识点
14.在锐角三角形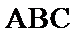

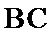
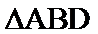
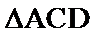
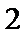
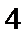
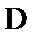
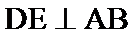
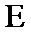
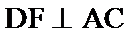
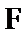
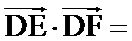
正确答案
解析
由题意得: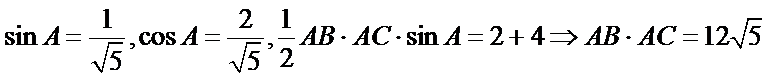
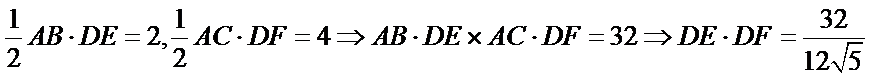
知识点
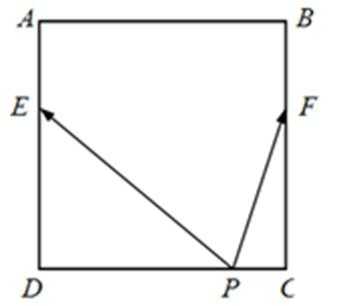
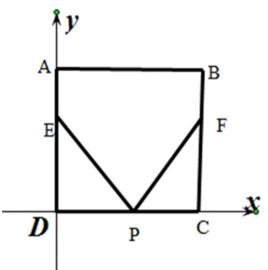
10.如图,正方形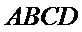
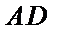
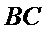
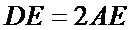
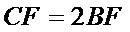
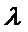
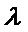
正确答案
解析
如图,
建立直角坐标系,则E(0,4)F(6,4)
(1)当P点在CD上时,设P(x,0)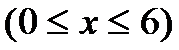
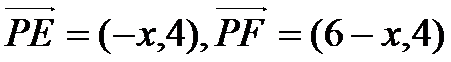
因为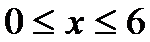
所以当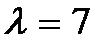
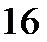
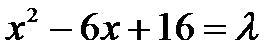
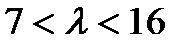
(2)当P点在AB上时,设P(x,6) 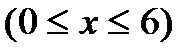
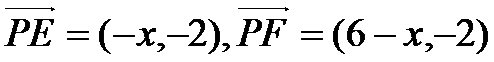
因为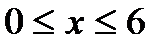
所以当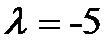
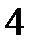
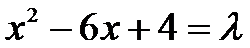
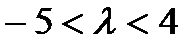
(3)当P点在AD上时(当P点在BC上的情况与在AD上相同),设P(0,y)
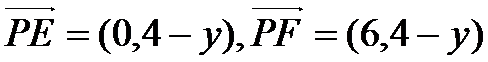
因为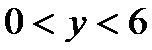
所以当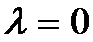
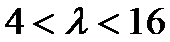
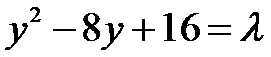
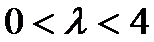
综上,当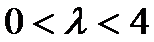
考查方向
解题思路
以D点为坐标原点建立直角坐标系,再分别讨论P点在AB,CD,以及AD和BC上的时候的情况,计算向量的数量积,并判断方程根的个数。(P在AD和BC上情况是一样的,不必分开讨论)
易错点
不能很好的判断方程根的个数
知识点
20.已知点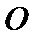
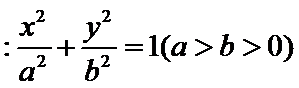
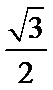
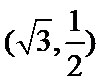
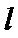
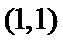
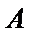
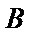
(I)求椭圆C的方程;
(Ⅱ)椭圆C上是否存在一点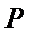
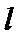
正确答案
(I)
(Ⅱ)存在直线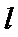
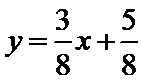
解析
(I)由题意得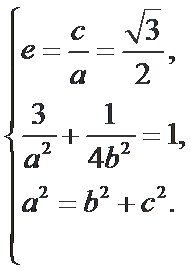
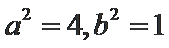
所以椭圆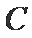
(Ⅱ)(1)当直线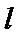
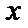
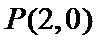
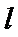
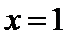
(2)当直线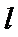
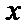
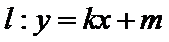
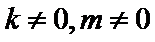
设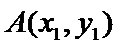
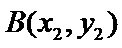
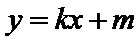
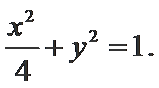
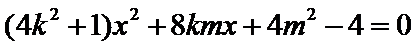
由直线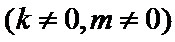
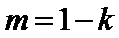
因此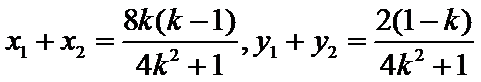
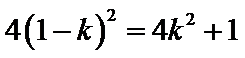
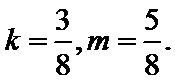
所以直线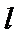
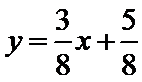
综上,椭圆C上存在点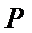
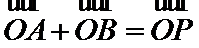
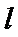
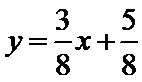
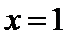
考查方向
解题思路
第一问直接根据离心率得到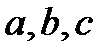
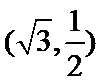
第二问设直线方程,别忘了考虑斜率不存在的情况,然后根据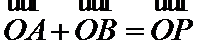
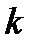
易错点
1、在第二问设斜率的时候没有考虑斜率不存在的情况;
2、在第二问中计算出错
知识点
7.如图,菱形





正确答案
解析
以点A坐标为原点建立如图所示的直角坐标系,因为菱形的边长为2,可以得到A(0,0),B(2,0),C



考查方向
解题思路
建立适当的坐标系,利用线性规划理论,求目标函数最大值
易错点
没能正确建立坐标系
知识点

设

正确答案
解析
这类题型需要建立好坐标系,根据坐标系找可行域更可行
考查方向
向
解题思路
先建立直角坐标系,然后求出EC和CD的方程,找到可行域,将平面向量用坐标形式表示,带入可行域中,求得。
易错点
建立坐标系错误、计算能力弱
知识点
扫码查看完整答案与解析