- 向量在几何中的应用
- 共173题
15.如图,菱形ABCD的边长为1,∠ABC=60°,E、F分别
为AD、CD的中点,则
正确答案
解析
考查方向
解题思路
本题考查了平面向量的数量积运算,可采用基向量法也可采用坐标法.基向量法需要选择合适的基底,
由于已知菱形的边长且


另外还可以尝试以

易错点
本题考查用基底表示时易错。
知识点
P是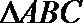
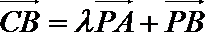
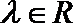
正确答案
解析
由已知,得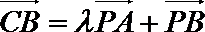
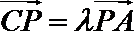
考查方向
本题主要考查了向量的基本运算以及平面几何的综合应用
易错点
向量基本运算需要仔细运算
知识点
16.已知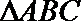
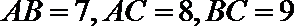
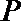
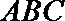
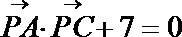
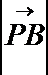
正确答案
10
解析
考查方向
本题主要考查了解三角形和平面向量及不等式
解题思路
本题考查解三角形和平面向量及不等式,解题思路如下:1、利用公式表示数量积;2、利用不等式求解。
易错点
本题必须注意数量积公式
知识点
4. 在





正确答案
解析
由

所以,
考查方向
本题考查了向量的线性运算及三角形法则等知识。
解题思路
由
易错点
向量的三角形法则不能熟练掌握,导致运算错误。
知识点
9.在△ ABC中,BC=5,G,O分别为AABC的重心和外心,且

正确答案
解析
在△ABC中,G、O分别为△ABC的重心和外心,取BC的中点为D,连接AD、OD、GD,则OD⊥BC,GD=





考查方向
本题主要考查向量数量积的性质和运用,主要考查向量的三角形法则,运用余弦定理判断三角形形状
解题思路
运用重心和外心的性质,可得

易错点
向量的加法运算和数量积不会应用
知识点
11.已知双曲线C的方程为


正确答案
解析
∵双曲线C的方程为
∴

所以MP平分


所以点M(2,1)就是
考查方向
本题主要考查双曲线几何性质和焦点三角形
解题思路
结合已知等式及平面几何知识得出点M是
易错点

知识点
8. 如图,正方形










正确答案
解析
以




(1)若点








(2)若点









(3)若点








(4)若点









综上所述,

考查方向
解题思路
1.建立直角坐标系,写出
2.分别讨论点




3.逐段得到
4.整合讨论结果,得到所求范围。
易错点
本题易在对

知识点
3.如图,正方形




正确答案
解析



考查方向
本题主要考察了平面向量的基本定理,属于中档题,是高考的热点,解决此类题的关键是会利用平面向量的基本定理,用两个不共线的向量表示平面内任一向量。
易错点
本题易在向量的表示过程中出现错误。
知识点
11.如图,在矩形OABC中,点E、F分别在线段AB、BC上,且满足




正确答案
解析
以
设
∵

∴
∵

∴
∴

得
解得
考查方向
本题考查了向量的坐标运算及平面向量分解定理,属于容易题,在近几年的各省高考题出现的频率较高,常与直线、圆锥曲线、数列、函数等知识点交汇命题.
解题思路
用坐标法求解;恰当选择新的基向量,寻找

易错点
题中所选的基向量不垂直,学生不容易找到相互之间的关系.
知识点
20. 已知



(I)求出动点P的轨迹对应曲线C的标准方程;
(II)一条纵截距为2的直线
(III)直线





正确答案
解: (Ⅰ) 因为
即
所以
所以
又因为
即:
所以椭圆的标准方程为
(Ⅱ) 直线

联立直线
得:
由
设
则
以
所以
即
也即
即
将(1)式代入,得
即
解得
(Ⅲ)由方程组
设
所以
因为直线
所以


不存在直线
解析
见答案
考查方向
本题主要考查动点的轨迹方程
解题思路
先求出动点运动的轨迹,然后判断是椭圆,然后根据椭圆的相关性质求解
易错点
找不到动点的运动规律,抓不住等量关系列出圆锥曲线方程,计算能力弱
知识点
扫码查看完整答案与解析