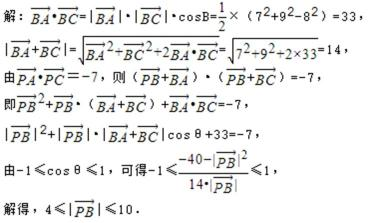- 向量在几何中的应用
- 共173题
16.已知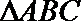
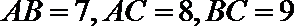
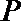
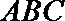
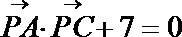
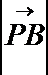
正确答案
10
解析
考查方向
本题主要考查了解三角形和平面向量及不等式
解题思路
本题考查解三角形和平面向量及不等式,解题思路如下:1、利用公式表示数量积;2、利用不等式求解。
易错点
本题必须注意数量积公式
知识点
4. 在





正确答案
解析
由

所以,
考查方向
本题考查了向量的线性运算及三角形法则等知识。
解题思路
由
易错点
向量的三角形法则不能熟练掌握,导致运算错误。
知识点
9.在△ ABC中,BC=5,G,O分别为AABC的重心和外心,且

正确答案
解析
在△ABC中,G、O分别为△ABC的重心和外心,取BC的中点为D,连接AD、OD、GD,则OD⊥BC,GD=





考查方向
本题主要考查向量数量积的性质和运用,主要考查向量的三角形法则,运用余弦定理判断三角形形状
解题思路
运用重心和外心的性质,可得

易错点
向量的加法运算和数量积不会应用
知识点
11.已知双曲线C的方程为


正确答案
解析
∵双曲线C的方程为
∴

所以MP平分


所以点M(2,1)就是
考查方向
本题主要考查双曲线几何性质和焦点三角形
解题思路
结合已知等式及平面几何知识得出点M是
易错点

知识点
8. 如图,正方形










正确答案
解析
以




(1)若点








(2)若点









(3)若点








(4)若点









综上所述,

考查方向
解题思路
1.建立直角坐标系,写出
2.分别讨论点




3.逐段得到
4.整合讨论结果,得到所求范围。
易错点
本题易在对

知识点
扫码查看完整答案与解析