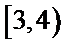- 离散型随机变量及其分布列、均值与方差
- 共221题
16.设矩形的长为




甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数,与标准值0.618比较,正确结论是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 方程
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
13.设函数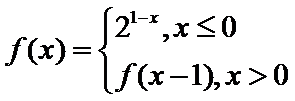
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
某公司向市场投放三种新型产品,经调查发现第一种产品受欢迎的概率为


(1)求该公司至少有一种产品受欢迎的概率;
(2)求
(3)求数学期望
正确答案
见解析。
解析
设事件




(1)由于事件“该公司至少有一种产品受欢迎”与事件“
所以该公司至少有一种产品受欢迎的概率是
(2)由题意知





(Ⅲ)由题意知


因此
知识点
某幼儿园为训练孩子的数字运算能力,在一个盒子里装有标号为1,2,3,4,5的卡片各两张,让孩子从盒子里任取3张卡片,按卡片上的最大数字的9倍计分,每张卡片被取出的可能性都相等,用X表示取出的3张卡片上的最大数字
(1)求取出的3张卡片上的数字互不相同的概率;
(2)求随机变量X的分布列及数学期望;
(3)若孩子取出的卡片的计分超过30分,就得到奖励,求孩子得到奖励的概率。
正确答案
见解析。
解析
(1)“一次取出的3张卡片上的数字互不相同”的事件记为A
则
(2)变量X的可能取值为2,3,4,5
所以分布列为
从而E(X)=2×



(3)“一次取卡片所得计分超过30分”的事件记为B
∴
∴孩子得到奖励的概率为
知识点
如图3,A,B两点之间有6条网线连接,每条网线能通过的最大信息量分别为1,1,2,2,3,4,从中任取三条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息量之和为
(1)当
(2)求
正确答案
见解析
解析
(1)解:从6条网线中随机任取三条网线共有





答:线路信息畅通的概率为
(2)解:ξ的取值为4,5,6,7,8,9.


∴ξ的的分布列为:


知识点
某批产品成箱包装,每箱5件,一用户在购进该批产品前先取出3箱,设取出的3箱中,第一、二、三箱中分别有0件、1件、2件二等品,其余为一等品。
(1)在取出的3箱中,若该用户从第三箱中有放回的抽取3次(每次一件),求恰有两次抽到二等品的概率;
(2)在取出的3箱中,若该用户再从每箱中任意抽取2件产品进行检验,用ξ表示抽检的6件产品中二等品的件数,求ξ的分布列及数学期望。
正确答案
见解析。
解析
(1)设A表示事件“从第三箱中有放回地抽取3次(每次一件),恰有两次取到二等品”,
依题意知,每次抽到二等品的概率为
故
(2)ξ可能的取值为0,1,2,3。
P(ξ=0)=


P(ξ=2)=




ξ的分布列为
数学期望为Eξ=1×


知识点
某班有甲、乙两个学习小组,两组的人数如下:
现采用分层抽样的方法(层内采用简单随机抽样)从甲、乙两组中共抽取
(1)求从甲组抽取的同学中恰有
(2)记


正确答案
见解析
解析
(1)解:依题意,甲、乙两组的学生人数之比为 
所以,从甲组抽取的学生人数为

设“从甲组抽取的同学中恰有

则 
故从甲组抽取的同学中恰有

(2)解:随机变量





所以,随机变量
………………11分

知识点
14.如图放置的正方形ABCD,AB =1.A,D分别在x轴、y轴的正半轴(含原点)上滑动,则
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
6.某班共30人,其中15人喜爱篮球运动,10人喜爱兵乓球运动,8人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为________。
正确答案
12
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析