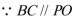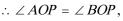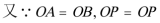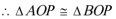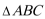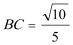- 圆的切线的判定定理的证明
- 共10题
22. 【选修4-1:几何证明选讲】
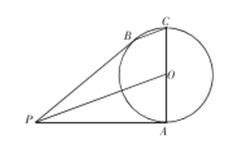
如图,已知线段AC为⊙O 的直径,P为⊙O的切线,切点为A,B为⊙O上一点,且BC∥PO.
( I )求证:PB为⊙O的切线;
(Ⅱ)若⊙O的半径为1,PA =3,求BC的长。
正确答案
(1)证明略;(2)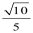
解析
试题分析:本题属于平面几何问题,题目难度较低,解题时要注意深入分析已知条件和特征结论,善于将各已知条件联系起来考虑,寻找合理的解题思路。
(1)连接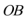
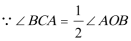
又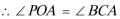
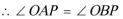
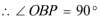
(2)连接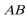
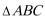
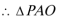
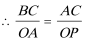
解得
考查方向
解题思路
本题考查三角形与圆的相关知识,解题步骤如下:
1、通过相应的条件和定理建立起有关角或边之间的关系式,如全等关系。
2、灵活三角形相似得到所需结论。
易错点
1、未想到连接OB、AB而无法下手;
2、第二问中由相似得到合适结论出错。
知识点
22. 如图,在直角








(Ⅰ)证明:
(Ⅱ)若



正确答案
(Ⅰ)略
(Ⅱ)
解析
试题分析:本题是有关直线与圆的问题,难度不大。在解题中注意结合切线的性质和勾股定理等知识进行解决。
(Ⅰ)
连结

因为

因为

所以
所以
(Ⅱ)由已知



所以
因为


因为

所以
考查方向
解题思路
本题主要考查圆的基本性质、圆周角定理等基础知识。解题步骤如下:
(Ⅰ)利用四点共圆的判定定理,证明
(Ⅱ)利用切线性质和勾股定理及第一问的结论,求出
易错点
第二问计算中,不易想到利用第一问
知识点
如图, 











正确答案
解析
略
知识点
AB是圆O的直径,D为圆O上一点,过D作圆O的切线交AB延长线于点C,若DA=DC,求证:AB=2BC。
正确答案
解析
(方法一)证明:连结OD,则:OD⊥DC,
又OA=OD,DA=DC,所以∠DAO=∠ODA=∠DCO,
∠DOC=∠DAO+∠ODA=2∠DCO,
所以∠DCO=300,∠DOC=600,
所以OC=2OD,即OB=BC=OD=OA,所以AB=2BC。
(方法二)证明:连结OD、BD。
因为AB是圆O的直径,所以∠ADB=900,AB=2 OB。
因为DC 是圆O的切线,所以∠CDO=900。
又因为DA=DC,所以∠DAC=∠DCA,
于是△ADB≌△CDO,从而AB=CO。
即2OB=OB+BC,得OB=BC。
故AB=2BC。
知识点
22.选修4-1:几何证明选讲
如图,












(Ⅰ)求证:

(Ⅱ)若

正确答案
见解析.
解析
试题分析:本题属于平面几何中的基本问题,题目的难度是容易题。
(Ⅰ)连接

又




(Ⅱ)过




设

由


可得
考查方向
本题考查了平面几何的知识,主要涉及直线与圆的位置关系,三角形相似的考查.
解题思路
本题考查平面几何的知识,解题步骤如下:利用圆的相关定理证明;利用切割线定理和相交弦定理证明。
易错点
相关的定理容易混用。
知识点
扫码查看完整答案与解析