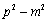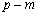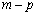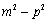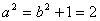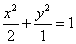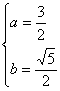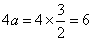- 椭圆的定义及标准方程
- 共573题
若椭圆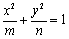
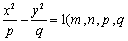
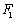
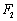
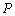
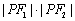
正确答案
解析
由题设可知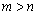
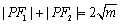
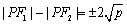
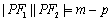
知识点
已知椭圆

(1)若原点到直线

(2)设过椭圆的右焦点且倾斜角为


i)当

ii)对于椭圆上任一点


正确答案
见解析
解析
(1)∵

∵

∵


椭圆的方程为
(2)
i)∵


易知右焦点


由①,②有:
设
∴
ii)显然




设
∵
又点

由③有:
则
……………⑤
又

将⑥,⑤代入④可得:
知识点
已知椭圆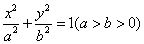
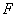
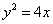
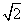
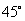
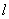
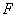
(1)求该椭圆的方程;
(2)设椭圆的另一个焦点为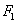
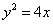
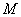
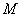
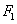
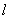
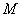
正确答案
见解析。
解析
(1)抛物线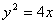
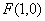
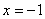
∴ 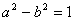
又椭圆截抛物线的准线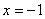
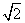
∴ 得上交点为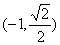
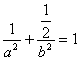
由①代入②得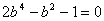
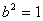
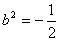
从而
∴该椭圆的方程为该椭圆的方程为
(2)∵ 倾斜角为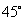
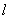
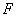
∴ 直线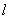
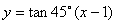
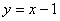
由(1)知椭圆的另一个焦点为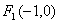
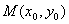
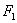
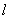
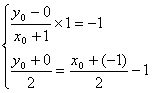
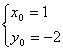
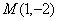
又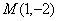
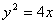
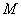
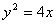
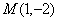
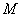
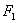
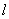
知识点
短轴长为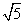
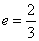
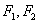
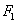
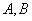
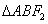
正确答案
6
解析
由题知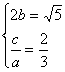
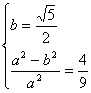
由椭圆的定义知△ABF2的周长为
知识点
已知椭圆





正确答案
解析
略
知识点
扫码查看完整答案与解析