- 椭圆的定义及标准方程
- 共573题
设椭圆C:

(1)求椭圆C的离心率;
(2)如果|AB|=
正确答案
(1)
解析
设


(1)直线l的方程为 

联立
解得
因为

即
得离心率 
(2)因为

由



椭圆C的方程为
知识点
如图,已知椭圆








(1)求椭圆和双曲线的标准方程;
(2)设直线




(3)是否存在常数


正确答案
见解析。
解析
(1)设椭圆的半焦距为


所以 

又

故椭圆的标准方程为
由题意设等轴双曲线的方程
因此 双曲线的标准方程为
(2)设
则 
因为 点


因此 
即 
(3)由于


由根与系数的关系得
所以

同理可得
则 
又 
所以 
故
因此 存在

知识点
现有10个数,它们能构成一个以1为首项,
正确答案
解析
∵以1为首项,
∴从这10个数中随机抽取一个数,它小于8的概率是
知识点
已知椭圆



(1)求椭圆
(2)设O为坐标原点,点A,B分别在椭圆



正确答案
见解析
解析
(1)由已知可设椭圆

其离心率为


故椭圆
(2)解法一 

由



因此可设直线

将



将



又由


解得 


解法二 

由



因此可设直线

将



又由


将



解得 


知识点
如图,在平面直角坐标系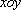
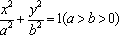
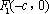
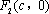
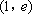
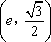

(1)求椭圆的方程;
(2)设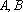

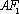
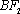
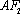
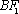
(i)若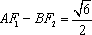
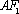
(ii)求证:
正确答案
见解析
解析
(1)根据椭圆的性质和已知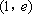
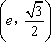
(2)根据已知条件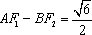
知识点
扫码查看完整答案与解析